Luận án Một số phụ thuộc logic mở rộng trong mô hình dữ liệu dạng khối

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
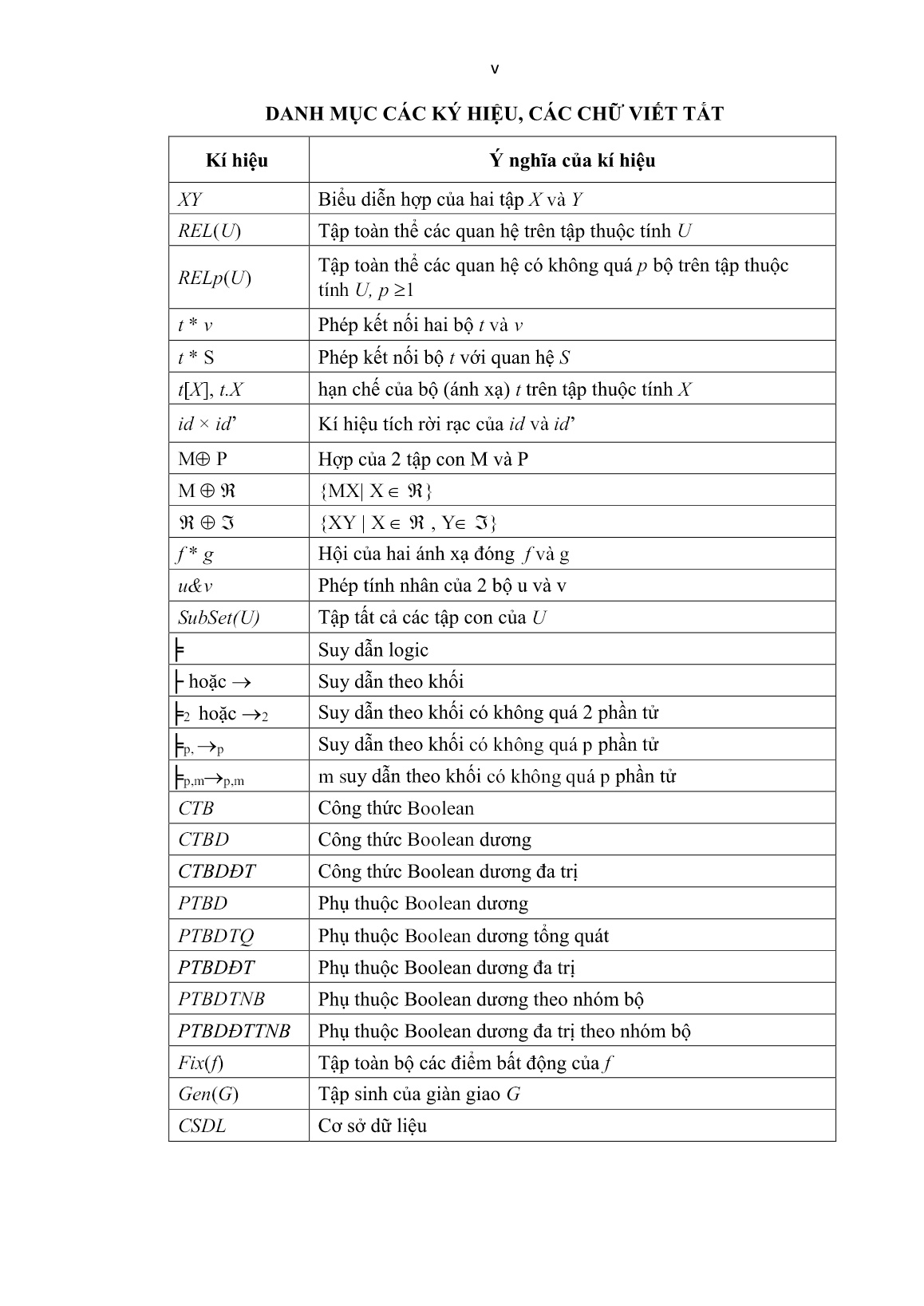
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Một số phụ thuộc logic mở rộng trong mô hình dữ liệu dạng khối", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Một số phụ thuộc logic mở rộng trong mô hình dữ liệu dạng khối

3), 3(2)3(4) 3(1),
3(1)3(4) 3(2), 3(1)3(2)3(3) 3(4)), 3(3)3(4) 3(1)3(2), 3(1)3(3)3(4) 3(2)}
Theo thuật toán XDF-S ta có:
1
n
x
i
F F
, ta thu được kết quả
0 1 0
1 0 0
0 0 0
0 0 0
0 0 0
0 1 0
0 1 0
1 0 0
1 0 0
A1 A2 A3
0 0
0
0 0 1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
A4
1
3/2019
1 1 0
1 1 0
1 0 1
1 0 1
1 1 0
1 1 0
1 1 0
1 1 0
2/2019
1 1
1
1 1 1
1
1
0
1
1
1
1
1
0
0
0
0
1
1
1 0 1 0
1/2019
44
F = {
1(2)1(3)1(4) 1(1), 1(2)1(3) 1(1)1(4), 1(4) 1(1)1(3), 1(2)1(4) 1(1),
1(1)1(4) 1(2), 1(1)1(2)1(3) 1(4), 1(3)1(4) 1(1)1(2), 1(1)1(3)1(4) 1(2),
2(2)2(3)2(4) 2(1), 2(2)2(3) 2(1)2(4), 2(4) 2(1)2(3), 2(2)2(4) 2(1),
2(1)2(4) 2(2), 2(1)2(2)2(3) 2(4), 2(3)2(4) 2(1)2(2), 2(1)2(3)2(4) 2(2),
3(2)3(3)3(4) 3(1), 3(2)3(3) 3(1)3(4), 3(4) 3(1)3(3), 3(2)3(4) 3(1),
3(1)3(4) 3(2), 3(1)3(2)3(3) 3(4), 3(3)3(4) 3(1)3(2), 3(1)3(3)3(4) 3(2)
}
2.3.3. Cài đặt thực nghiệm thuật toán XDF
- Mục tiêu: Tìm Hội suy dẫn trên khối qua một khối chân lý cho trước.
- Công cụ và môi trường thực nghiệm:
Công cụ để xây dựng chương trình: Ngôn ngữ lập trình PHP, Javascript.
Môi trường thực nghiệm: Máy tính PC cấu hình Intel(R) Core™ i7 2.5Ghz,
RAM 8G, Windows 10 OS.
- Chạy thực nghiệm chương trình:
Đầu vào: Khối nhị phân T ở ví dụ 2.4.
Đầu ra: Hội suy dẫn F nhận khối nhị phân T làm khối chân lý.
- Kết quả chạy chương trình:
Tìm được Hội suy dẫn F = {
1(4) 1(1), 2(4) 2(1), 3(4) 3(1),
1(3)1(4) 1(1)1(2), 2(3)2(4) 2(1)2(2), 3(3)3(4) 3(1)3(2),
1(2)1(4) 1(1), 2(2)2(4) 2(1), 3(2)3(4) 3(1),
1(2)1(3) 1(1), 2(2)2(3) 2(1), 3(2)3(3) 3(1),
1(2)1(3)1(4) 1(1), 2(2)2(3)2(4) 2(1), 3(2)3(3)3(4) 3(1),
1(1)1(3)1(4) 1(2), 2(1)2(3)2(4) 2(2), 3(1)3(3)3(4) 3(2)
}
- Đánh giá thực nghiệm và ý nghĩa thực tiễn:
Thuật toán tính đúng Hội suy dẫn. Thời gian chạy thực hiện thuật toán:
0.014756000041962 mins.
45
Chạy thực nghiệm với các khối chân lý khác, tính đúng kết quả theo thuật
toán, từ đó khẳng định, chương trình chạy thực nghiệm tìm hội suy dẫn, đúng theo
thuật toán XDF.
2.4. Phụ thuộc Boolean dương đa trị trong mô hình dữ liệu dạng khối
2.4.1. Khối m-chân lý của khối dữ liệu
Định nghĩa 2.4
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
,
id s , ta gọi mỗi vector các phần tử 1 2 1.., , ..., i i in i sv v v v trong không gian
n s
B là một phép gán trị.
Như vậy, với mỗi CTBĐT f MVL U ta có 1 2 1.. , ,...,i i in i tf v f v v v
là trị của công thức f đối với phép gán trị v.
Ví dụ 2.6:
Cho 1 2 31,2 , , , R A A A , khi đó ( ) ( )1 2 3 1 2( 3) ( ) ( ) ( )1 , 1 , 1 , 2 , 2 , 2U ,
0, 0.5, 1 . B
Cho
0.5 1 0.5
1 0.5 0.5
v
, ( ) ( ) ( )1 2 1 2( ) ( 3( )3) 1 1 2 2 1 2f , khi đó ta có
1 0.5, 1, 1, 0.5 , 0.5, 0.5f v max min min .
Suy ra : 0.5f v .
Ta có hai phép gán trị đặc biệt:
Phép gán trị đơn vị:
1 1 1
. . .
1 1 1
e
, và phép gán trị 0:
0 0 0
. . .
0 0 0
z
Định nghĩa 2.5
Cho 0 ;1m , khối chân lý ngưỡng m của f hoặc khối m-chân lý của f, kí
hiệu ,f mT là tập các phép gán trị v sao cho f(v) nhận giá trị không nhỏ thua m:
, { } |
n s
f mT v f v m
B
46
Khi đó, khối m-chân lý
,F mT của tập hữu hạn các công thức F trên U, chính
là giao của các khối m-chân lý của mỗi công thức thành viên f trong F.
, ,F m f m
f F
T T
.
Ta có:
,F mv T khi và chỉ khi : f F f v m .
Với | | k B thì khi đó | =|n s n sk B , ta có định lý sau:
Ví dụ 2.7. Để so sánh các tập tài liệu được thu thập vào các thời điểm khác
nhau xem chúng giống nhau hay khác nhau như thế nào, có phải là cùng được in từ
nhà xuất bản hay không, ta phân loại như sau:
A1: Loại giấy in (T: Tốt; M: Trung Bình; S: Kém)
A2: Mực in (T: Tốt; M: Trung Bình; S: Kém)
A3: Nội dung in (T: giống nhau 100%; M: chỉ khoảng 50%; S: không giống nhau).
Ta xây dựng khối R và định nghĩa phép gán trị như sau:
Cho 1 2 3 1,2 , , , R A A A , U = {1(1), 1(2), 1(3), 2(1), 2(2), 2(3)}, B ={0, 0.5, 1}.
Với thuộc tính A1, nếu loại giấy in tốt ta gán là 1, trung bình ta gán là 0.5,
kém ta gán là 0 tương ứng với các mức trong tập trị B;
Với thuộc tính A2, nếu loại mực in tốt ta gán là 1, trung bình ta gán là 0.5,
kém ta gán là 0 tương ứng với các mức trong tập trị B;
Với thuộc tính A3, nếu nội dung giống nhau ta gán là 1, nội dung chỉ xem
được khoảng 50% thì ta gán là 0.5, nội dung khác nhau ta gán là 0 tương ứng với
các mức trong tập trị B;
Cho phép gán trị
0.5 1 0.5
1 0.5 1
v
, khi đó ta có:
Với F(v): 1(1) 1(2) 1(3) 2(1) 2(2) 2(3) = 0.5, như vậy các tài liệu này chỉ
được đánh giá giống nhau 50%, có nghĩa là chúng giống nhau ở mức độ 0.5. Khi đó
công thức 1(1) 1(2) 1(3) 2(1) 2(2) 2(3) là công thức Boolean đa trị trong mô hình
dữ liệu dạng khối.
47
Với F(v) : 1(2) ( 2(3)) = 0, khi đó công thức 1(2) ( 2(3)) không phải là
công thức Boolean đa trị trong mô hình dữ liệu dạng khối.
Định lý 2.4
Với mỗi khối 1 2, , ,
n s
dT t t t
B và mỗi dãy trị
1 2, , , dm m m
trong B , 1
n sd k , tồn tại một CTBĐT f thỏa hai tính chất sau:
(i) =:i i it T f t m ,
(ii) :\ 0.n st T f t B
Chứng minh:
Với mỗi 1 2 1..: , , ..., i i ij ij ijn j st T t t t t , 1 i d , ta xây dựng công thức:
( ) ( ) ( ) ( ) ( ) (1 2 1 21 21 . 1..
)
.
, , , , , , , j j jn j j jni tij tij tijn ij s j s
h x x x I x I x I x m
khi đó nếu 1 2 1 2 1..1.
) (
.
( ) ( ), , , , , ..., j j jn i ij ij ijn j sj s
x x x t t t t
thì i i ih t m ,
0ih t với , 1it t i d .
Do vậy, nếu ta đặt: 1 2( ) ( ) ( ) 1 21.., , ,
j j jn
dj s
f x x x h h h
thì f chính
là công thức cần tìm.
Thật vậy, ta có:
1 2 1 2( ) i d i i i i i d if t h h h t h t h t h t h t
Mà theo tính chất của
ih :
1 2 1 1 2 2 1..1.. ( ), , ..., , , , , i i ij ij ijn tij ij tij ij tijn ijn i j s ij sh t h t t t I t I t I t m m
0ih t với , 1it t i d .
Vậy suy ra: , 1 \ : 0n si if t m i d và t T f t
B f chính là
CTBĐT cần tìm.
48
Hệ quả 2.3:
Với mỗi khối
n sT B , T và mỗi trị m>0 trong B, tồn tại một CTBĐT
f nhận T làm khối m-chân lý, tức là ,f mT T .
Chứng minh:
Sử dụng kết quả của định lý 3.1 với trường hợp đặc biệt:
1 2 dm m m m ta thu được CTBĐT f thỏa mãn hai điều kiện:
(i) : i i it T f t m ,
(ii) \ : 0n st T f t B .
Từ đó suy ra: ,f mT T .
2.4.2. Công thức Boolean dương đa trị
Định nghĩa 2.6
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, mỗi
CTBĐT f MVL(U) được gọi là công thức Boolean dương đa trị (CTBDĐT) nếu
f(e) = 1, với e là phép gán trị đơn vị. Ở đây:
1 1 1
. . .
1 1 1
e
Ví dụ 2.8:
Cho 1 2 3 1,2 , , , R A A A , U = {1(1), 1(2), 1(3), 2(1), 2(2), 2(3)},
B ={0, 0.5, 1}.
Khi đó: với phép gán trị đơn vị e ta có:
- Các công thức: 1(1) 1(2) 2(1) 2(2), 1(1) 1(2) 2(1) 2(2) là các CTBDĐT.
- Các công thức: 1(2) (2(3)), (1(3)) (2(1)) không phải là các CTBDĐT.
49
Định nghĩa 2.7
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R, ta kí hiệu di là miền
trị của thuộc tính Ai (cũng là của thuộc tính chỉ số x(i), x id), 1 i n. Khi đó, với
mỗi miền trị di ta xét ánh xạ: : i i id d B thỏa các điều kiện sau:
(i) Tính phản xạ: : , 1i ia d a a ,
(ii) Tính đối xứng: , : , ,i i ia b d a b b a ,
(iii) Tính đầy đủ: m B, a, b di: i(a,b) = m.
Như vậy, ta thấy các ánh xạ i chính là các quan hệ trên di thỏa các tính chất
phản xạ, đối xứng và đầy đủ. Quan hệ đẳng thức với logic hai trị 0,1B là
trường hợp riêng của quan hệ trên.
2.4.3. Phép gán trị
Định nghĩa 2.8
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R, u,v r, các ánh xạ
i xác định trên mỗi miền trị di, 1 i n. Ta gọi (u,v) là phép gán trị:
1( ) ( ) ( ) ( ) ( ) ( )1 2 21 2, . , . , . , . ,..., . , . .n nn
x id
u v u x v x u x v x u x v x
Khi đó, với mỗi khối r ta kí hiệu khối chân lý của khối r là
rT :
, | , .rT u v u v r
Nếu khối r có chứa ít nhất một phần tử u nào đó thì: , ru u e e T .
Trong trường hợp tập id = {x}, khi đó khối suy biến thành quan hệ và khái
niệm khối chân lý của khối lại trở thành khái niệm bảng chân lý của quan hệ trong
mô hình dữ liệu quan hệ. Nói một cách khác, khối chân lý của khối là mở rộng khái
niệm bảng chân lý của quan hệ trong mô hình dữ liệu quan hệ.
Ví dụ 2.9: Cho khối dữ liệu R = ({1, 2, 3}; A1, A2, A3), r là một khối trên R,
trong đó id ={1, 2, 3} là thuộc tính chỉ số tương ứng là Mùa hè, Mùa xuân, Mùa
đông. Tập trị B ={0, 0.3, 0.7, 1}. Ta kí hiệu A1: Bánh mì, A2: Bơ, A3: Sữa là các
thuộc tính của khối được gán trị như hình 2.8:
50
r: Ban_hang_DT
Hình 2.5: Khối dữ liệu Ban_hang_DT
Đặt phép gán trị các cặp phần tử: (a, b); với a, b là giá trị của loại hàng
(CC, L1, L2). Ta quy ước phép gán trị:
(a, b) = 1 nếu a = b;
(a, b) = 0.7 nếu a và b có đôi 1 khác nhau;
(a, b) = 0.3 nếu hoặc có a hoặc có b;
(a, b) = 0 nếu a = null và b = null.
Mùa đông (3)
L2 L2
CC L2
CC CC
CC null
L2 L2
L2 L2
CC CC
CC CC
CC L2
Bánh mì
(A1)
Bơ
(A2)
Mùa xuân (2)
Mùa hè (1)
t1
t2
t3
L2
L2
L2 null
null
L2
t4
CC
null
L2
null
L2
L2
CC
null
CC
L2
L2
Sữa
(A3)
L2
L2
L2
L2 null
null tn
L1
null
L1
L1
51
Khi đó, kết quả phép gán trị trên khối Tr thu được như hình 2.10:
Tr
Hình 2.6: Khối chân lý Tr
Nhận xét: Qua khối chân lý Tr, mối quan hệ mức tiêu thụ giữa bánh mì, bơ và
sữa trong Mùa hè như sau:
- Cứ 4 cặp mua bánh mì (cùng loại hàng CC hoặc L1 hoặc L2) thì có 1 cặp
mua bơ hoặc sữa (cùng loại hàng CC hoặc L1 hoặc L2).
- Cứ 10 cặp mua bánh mì (không phân biệt loại hàng) thì có 3 cặp mua bơ
Mùa đông (3)
0.7 0.3
0.7 0.7
1 0.7
1 0.3
0.7 1
0.7 0.3
1 0.3
0.7 0.3
0.7 0.7
Bánh mì
(A1)
Bơ
(A2)
Mùa xuân (2)
Mùa hè (1)
(t1, t2)
0.7
0.7
1 0.3
0.3
0.7
0.3
1
0.7
0.3
0.3
0.3
0.3
0.3
0.7
0.7
0.3
Sữa
(A3)
0.3
1
1
1 0
0
0.7
0
0.7
0.7
1 0.3
0.7 0.3
0.7 0.3
0.7 0.7
0.7 0.3
1 1
0.7 0.3
0.7 0.7
0.7 0.3
1
1
0.7 0.3
0.3
0.7
0.7
0.3
0.3
0.3
0.7
1
0.7
0.7
0.3
0.3
0.3
0.7
0.7 1
0.7 0.7
1 0.7 0.3
0.7
1
(t1, t3)
(t1, t4)
(t1, tn)
(t2, t3)
(t2, t4)
(t2, tn)
(t3, t4)
(t3, tn)
(t4, tn)
52
(không phân biệt loại hàng CC, L1, L2), 6 cặp mua sữa (không phân biệt loại hàng
CC, L1, L2).
Căn cứ vào số liệu trên, ta thấy vào mùa hè khách hàng có xu hướng mua
bánh mì kèm theo sữa nhiều hơn so với mua kèm bơ, tương tự như vậy với mùa
xuân và mùa đông khách hàng có xu hướng mua bánh mì kèm bơ nhiều hơn so với
mua kèm sữa.
Với kết quả trên, sẽ là cơ sở để giúp nhà quản lý biết được mức tiêu thụ và tỉ
lệ mua hàng của khách hàng ứng với từng mùa, để từ đó cân đối việc nhập hàng và
sắp xếp hàng hóa được hợp lý.
2.4.4. Phụ thuộc Boolean dương đa trị trên khối
Định nghĩa 2.9
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, ta gọi
mỗi công thức Boolean dương đa trị trong MVP(U) là một phụ thuộc Boolean
dương đa trị (PTBDĐT) trên khối.
Ta nói khối r m-thỏa phụ thuộc Boolean dương đa trị f và kí hiệu r(f,m) nếu
,r f mT T .
Khối r m-thỏa tập phụ thuộc Boolean dương đa trị F và kí hiệu r(F,m) nếu
khối r thỏa mọi PTBDĐT f trong F:
,, : , r F mr F m f F r f m T T .
Nếu có ,r f m ta cũng nói PTBDĐT f m-đúng trong khối r.
53
Ví dụ 2.10:
Cho khối dữ liệu R = ({1, 2, 3}; A1, A2, A3), r là một khối trên R đã cho ở ví
dụ 2.9.
r:
Yêu cầu: Tìm phụ thuộc dữ liệu trên các thuộc tính A1, A2, A3 (cũng là của
thuộc tính chỉ số x(i), x id).
Với quy ước phép gán trị các cặp các phần tử đã cho ở như ví dụ 2.9:
(a, b) = 1 nếu a = b;
(a, b) = 0.7 nếu a và b có đôi 1 khác nhau;
(a, b) = 0.3 nếu hoặc có a hoặc có b;
(a, b) = 0 nếu a = null và b = null.
Giả sử, xét các công thức trên các thuộc tính A1, A2, A3 (cũng là của thuộc
tính chỉ số x(i), x id): x(1) x(2); x(1) x(2)x(3); x(1) x(2)x(3).
Mùa đông (3)
L2 L2
CC L2
CC CC
CC null
L2 L2
L2 L2
CC CC
CC CC
CC L2
Bánh mì
(A1)
Bơ
(A2)
Mùa xuân (2)
Mùa hè (1)
t1
t2
t3
L2
L2
L2 null
null
L2
t4
CC
null
L2
null
L2
L2
CC
null
CC
L2
L2
Sữa
(A3)
L2
L2
L2
L2 null
null tn
L1
null
L1
L1
54
Ta lập khối chân lý Tf,m gồm các thuộc tính A1, A2, A3 (cũng là của thuộc tính
chỉ số x(i), x id) và các thuộc tính là công thức: x(1) x(2); x(1) x(2)x(3);
x(1) x(2)x(3), với m = 0.7.
Ta được khối chân lý Tf,m như hình 2.10:
Tf,m :
Hình 2.7: Khối chân lý Tf,m
Mùa đông (3)
0.7 0.3
0.7 0.7
1 0.7
1 0.3
0.7 1
0.7 0.3
1 0.3
0.7 0.3
0.7 0.7
Bánh mì
(A1)
Bơ
(A2)
Mùa xuân (2)
Mùa hè (1)
(t1, t2)
0.7
0.7
1 0.3
0.3
0.7
0.3
1
0.7
0.3
0.3
0.3
0.3
0.3
0.7
0.7
0.3
Sữa
(A3)
0.3
1
1
1 0
0
0.7
0
0.7
0.7
1 0.3
0.7 0.3
0.7 0.3
0.7 0.7
0.7 0.3
1 1
0.7 0.3
0.7 0.7
0.7 0.3
1
1
0.7 0.3
0.3
0.7
0.7
0.3
0.3
0.3
0.7
1
0.7
0.7
0.3
0.3
0.3
0.7
0.7 1
0.7 0.7
1 0.7 0.3
0.7
1
(t1, t3)
(t1, t4)
(t1, tn)
(t2, t3)
(t2, t4)
(t2, tn)
(t3, t4)
(t3, tn)
(t4, tn)
1 1
1 1
0 0
0 0
0 1
1 1
0 1
1 1
1 1
x(1) x(2
)
x(1) x(2) x(3)
1
1
0 0
1
1
1
1
1
1
1
1
1
1
1
1
1
x(1) x
(2) x(3)
1
1
1
1 1
1
1
1
1
1
0 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
0
0
1 1
0
1
1
1
1
1
1
1
1
1
1
1
1
0
0 1
1 1
0 0 1
1
1
55
- Xét công thức: f: x(1) x(2) :
+ Với lắt cắt 1: Do có các cặp phần tử: (t1, t2) = 0, (t2, t3) = 0, (t3, t4) = 0,
(t3, tn) = 0;
+ Tương tự các lát cắt 2 và lát cắt 3, tồn tại cặp phần tử có phép gán trị = 0.
Do đó Tr Tf. Suy ra không tồn tại phụ thuộc hàm từ x(1) x(2) hay
(1) (2)notx x . Nói cách khác r không thỏa phụ thuộc hàm f.
- Xét công thức Boolean: f: x(1) x(2) x(3) :
+ Với lắt cắt 1: Do có các cặp phần tử: (t1, t2) = 0, (t3, tn) = 0;
+ Tương tự các lát cắt 2 và lát cắt 3, tồn tại cặp phần tử có phép gán trị = 0.
Do đó Tr Tf. Suy ra không tồn tại phụ thuộc Boolean dương x(1) x(2) x(3)
hay (1) (2) (3)notx x x . Nói cách khác r không thỏa phụ thuộc Boolean dương f.
- Xét công thức Boolean: f: x(1) x(2) x(3):
+ Với lắt cắt 1: Phép gán trị các cặp phần tử tùy ý đều bằng 1
+ Tương tự như vậy với các lát cắt 2 và lát cắt 3 cũng tồn tại các cặp phần tử
với phép gán trị = 1.
Do đó Tr Tf. Theo Định nghĩa 2.9 thì tồn tại phụ thuộc Boolean dương đa
trị x(1) x(2) x(3) trên khối. Nói cách khác r thỏa phụ thuộc Boolean đa trị f trên
khối theo ngưỡng m = 0.7 hay r m-thỏa phụ thuộc Boolean dương đa trị f, m = 0.7.
Nhận xét: Với khối dữ liệu đã cho ở ví dụ 2.9, luận án chỉ ra rằng, không tồn
tại Phụ thuộc hàm trên khối, cũng không tồn tại phụ thuộc Boolean dương trên khối,
mà tồn tại phụ thuộc Boolean dương đa trị trên khối (thông qua việc mở rộng phép
sánh trị các cặp phần tử). Hay nói cách khác, với phụ thuộc hàm và phụ thuộc
Boolean dương trên khối mà các nghiên cứu trước đó không tìm được ràng buộc dữ
liệu giữa các mặt hàng bánh mì, bơ và sữa. Bằng việc mở rộng phép sánh trị mà
luận án đề xuất, các mặt hàng bánh mì, bơ và sữa lại tồn tại ràng buộc dữ liệu. Kết
quả đạt được, giúp các nhà quản lý bán hàng có thể theo dõi được xu hướng khách
hàng mua hàng theo mùa và thường mua kèm mặt hàng nào, với tỉ lệ nào.
Từ các khái niệm được đề xuất ở trên, ta có định lý tương đương sau:
56
Định lý 2.5
Cho tập PTBDĐT F và một PTBDĐT f , 1 2 ; , ,..., nR id A A A , r(R) là một
khối trên R, m B . Khi đó ba mệnh đề sau là tương đương:
(i)
m
F f (suy dẫn logic),
(ii)
m
F f (suy dẫn theo khối),
(iii)
2,m
F f (suy dẫn theo khối có không quá 2 phần tử).
Chứng minh:
(i) (ii): Theo giả thiết ta có , ,F m f mmF f T T
(1) . Giả sử r là một
khối bất kì và ,r F m , khi đó theo định nghĩa: ,r F mT T (2). Từ (1) và (2) ta suy
ra: ,r f mT T , vậy ta có: ,r f m .
(ii) (iii): Hiển nhiên, vì suy dẫn theo khối có không quá 2 phần tử là
trường hợp đặc biệt của suy dẫn theo khối.
(iii) (i): Giả sử (1 2( ( ) ,) ) , , ..., , n F mx idt x x x t T , ta cần chứng
minh ,f mt T .
Thật vậy, nếu t = e thì ta có ngay ,f mt T vì như ta đã biết f là công thức
Boolean dương. Nếu t e , ta xây dựng khối r gồm 2 phần tử u và v như sau:
1( ) ( (2) ) , ,..., n
y id
u y y y
, 1 2( ) ( ) ( ) , ,..., n
z id
v z z z
sao cho ,a u v t
(nghĩa là ( ) ( ), ,1i ii ia y z t i n ). Sự tồn tại của các phần tử u và v như trên là
do tính chất của các ánh xạ i đã nói tới ở trên. Như vậy r là khối có 2 phần tử và
,, r F mT e t T , với e là phần tử của khối mà mọi giá trị thành phần đều bằng 1.
Từ đó suy ra ,r F m . Theo giả thiết thì từ , ,r F m r f m , do đó
, r f mT T
(1) .
Từ bao hàm thức (1) ta suy ra ,f mt T .
57
Trong trường hợp tập { }id x , khi đó khối suy biến thành quan hệ và định
lý m-tương đương ở trên lại trở thành định lý tương đương trong mô hình dữ liệu
quan hệ. Cụ thể, ta có hệ quả sau:
Hệ quả 2.4
Cho tập PTBDĐT F và một PTBDĐT f , 1 2 ; , ,..., nR id A A A , r(R) là
một khối trên R, m B . Khi đó nếu { }id x thì khối r suy biến thành quan hệ và
ba mệnh đề sau là tương đương:
(i)
m
F f (suy dẫn logic),
(ii)
m
F f (suy dẫn theo quan hệ),
(iii)
2,m
F f (suy dẫn theo quan hệ có không quá 2 phần tử).
2.4.5. Bao đóng tập phụ thuộc Boolean dương đa trị
Định nghĩa 2.10
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, m B ,
là tập con các PTBDĐT trên U, ta kí hiệu (,m)+ là tập tất cả các PTBDĐT được
m-suy dẫn từ , nói một cách khác:
, ,( ) { | } {, | } m g mmm g MVP U g g MVP U T T
.
Định nghĩa 2.11
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, m B
ta kí hiệu MBDĐT(r,m) là tập tất cả các PTBDĐT m-đúng trong r, nói một cách khác:
, | ,MBDĐT r m g MVP U r g m
Như vậy, ta có: ,, r g mg MBDĐT r m g MVP U T T .
Định lý 2.6
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, m B .
Khi đó ta có: , , ,MBDĐT r m m MBDĐT r m
.
58
Chứng minh:
Theo định nghĩa, ta có:
, ,{ | },
m
MBDĐT r m m g MVP U MBDĐT r m g
(1)
Áp dụng kết quả của định lý ba mệnh đề tương đương cho PTBDĐT, ta lại có:
| , ,| ( )m mg MVP U MBDĐT r m g g MVP U MBDĐT r m g (2)
Từ (1) và (2) ta suy ra: , , ,MBDĐT r m m MBDĐT r m
.
Vậy hai tập , ,MBDĐT r m m
và ,MBDĐT r m là hai tập PTBDĐT
m-tương đương trên khối.
Hệ quả 2.5
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R, m B . Khi đó, nếu
id x thì khối r suy biến thành quan hệ và ta có trong mô hình dữ liệu quan hệ:
, , ,MBDĐT r m m MBDĐT r m
.
2.4.6. Thể hiện và thể hiện chặt tập phụ thuộc Boolean dương đa trị
Định nghĩa 2.12
Cho 1 2 ; , ,..., nR id A A A , r(R) là một khối trên R,
( )
1
n
i
i
U id
, m B ,
là tập con các PTBDĐT trên U.
Ta nói khối r là m-thể hiện tập nếu ), ,(MBDĐT r m m và khối r là
m-thể hiện chặt tập nếu , ,( )MBDĐT r m m .
Nếu khối r là m-thể hiện chặt tập PTBDĐT thì ta nói r là khối m-
Armstrong của tập PTBDĐT .
Định lý 2.7
Cho 1 2 ; , ,..., nR id A A A , m B . Khi đó, với mọi khối r(R) khác rỗng
trên R ta có: , , r MBDĐT r m mT T .
59
Chứng minh:
Giả sử , g MBDĐT r m r là m-thỏa ,r g mg T T . Từ khối Tr và
giá trị m, theo định lý 2.1 ta tìm được một công thức Boolean đa trị f thỏa điều kiện:
1f e và ,f m rT T . Như vậy: , r f me T T nên f là một CTBDĐT và hơn nữa
do ,r f mT T r là m-thỏa f, nghĩa là: ,f MBDĐT r m .
Ta kí hiệu: ,F MBDĐT rFile đính kèm:
 luan_an_mot_so_phu_thuoc_logic_mo_rong_trong_mo_hinh_du_lieu.pdf
luan_an_mot_so_phu_thuoc_logic_mo_rong_trong_mo_hinh_du_lieu.pdf Danh muc cong trinh cong bo.pdf
Danh muc cong trinh cong bo.pdf Đóng góp mới TA và TV NCS Trinh Ngọc Truc_0001.pdf
Đóng góp mới TA và TV NCS Trinh Ngọc Truc_0001.pdf Nhung dong moi cua luan an - Tieng Anh.pdf
Nhung dong moi cua luan an - Tieng Anh.pdf Nhung dong moi cua luan an - Tieng Viet.pdf
Nhung dong moi cua luan an - Tieng Viet.pdf QĐ 1924 HD cap Hoc vien ngay 21.12.21_TNT.pdf
QĐ 1924 HD cap Hoc vien ngay 21.12.21_TNT.pdf Tom tat luan an - Tieng Anh.pdf
Tom tat luan an - Tieng Anh.pdf Tom tat luan an - Tieng Viet.pdf
Tom tat luan an - Tieng Viet.pdf Trang thông tin đóng góp mới TA và TV, trích yếu LA Tran Huy Duong_0001.pdf
Trang thông tin đóng góp mới TA và TV, trích yếu LA Tran Huy Duong_0001.pdf Trích yếu luận án TNT_0001.pdf
Trích yếu luận án TNT_0001.pdf Trich yeu luan an.docx
Trich yeu luan an.docx Trich yeu luan an.pdf
Trich yeu luan an.pdf

