Luận án Nghiên cứu, ứng dụng năng lượng điện cảm trên ô tô

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
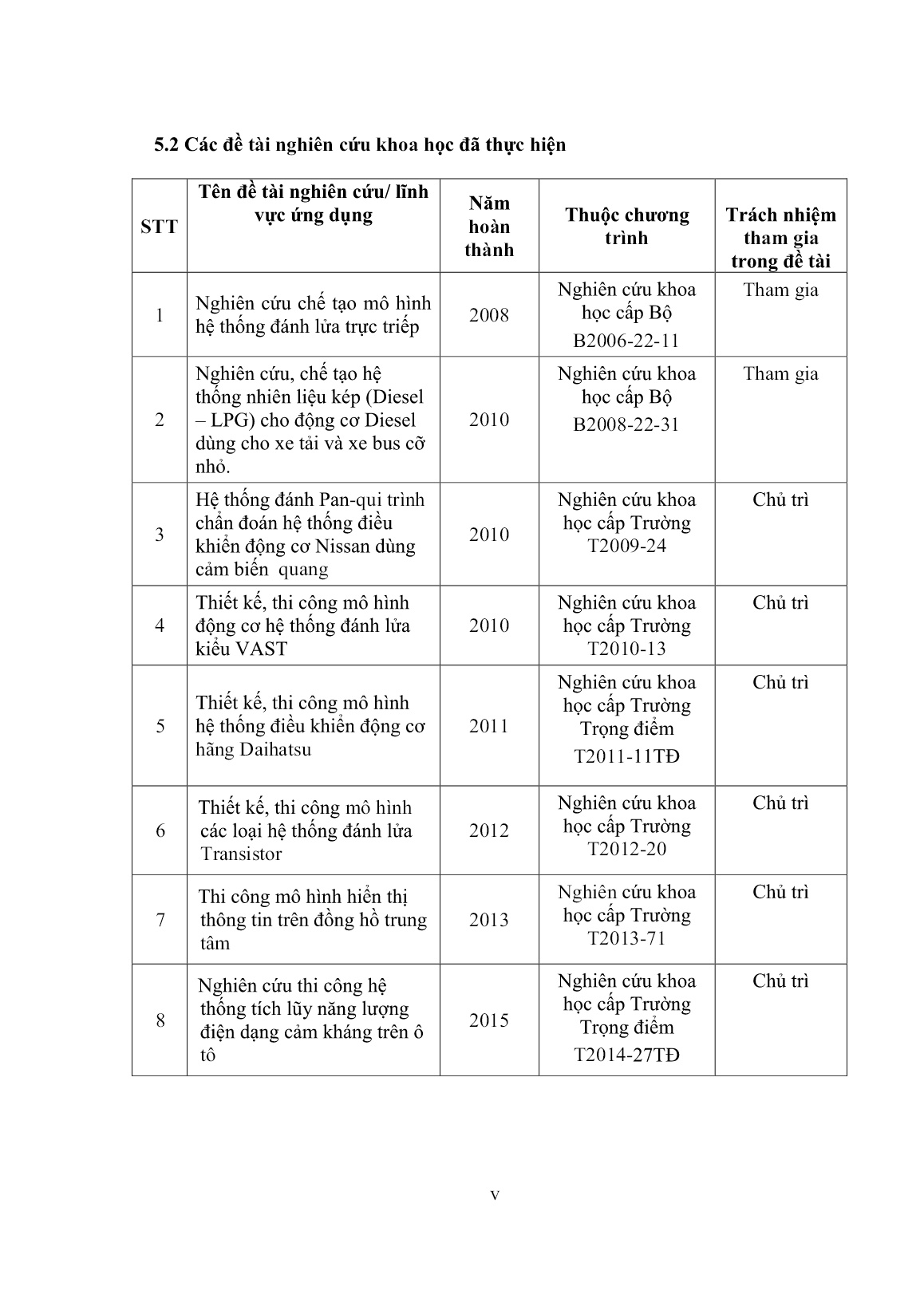
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu, ứng dụng năng lượng điện cảm trên ô tô", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu, ứng dụng năng lượng điện cảm trên ô tô

0 4500 5000 5500 6000
N
ăn
g
l
ư
ợ
n
g
đ
iệ
n
c
ảm
(
j)
Tốc độ động cơ (vòng/phút)
Năng có khả năng thu hồi trên bobine
Năng có khả năng thu hồi trên kim phun
42
Nhận định: nguồn năng lượng có thể thu hồi được của kim phun là rất thấp (0,1%) so
với bobine (99%) tại cùng dải tốc độ động cơ. Đây là thông tin người nghiên cứu cần
quan tâm và xác định mục tiêu sẽ chỉ triển khai thu hồi năng lượng trên cuộn sơ cấp
bobine.
2.5 Tính toán trên hệ siêu tụ
2.5.1 Mô hình hóa hệ siêu tụ
Theo phân tích tại mục 2.2.6, các xung điện động tuy có biên độ rất lớn nhưng thời
gian xuất hiện rất ngắn. Vì vậy, để lưu trữ năng lượng từ các xung điện động này cần
có một bộ lưu trữ năng lượng có khả năng nạp, xả rất nhanh đủ để đáp ứng quá trình
phóng nạp của các xung điện động. Ở đây, người nghiên cứu lựa chọn một hệ siêu tụ
điện làm một nguồn thứ cấp để lưu trữ năng lượng dạng điện cảm từ các cuộn cảm
trên hệ thống điện ô tô.
Một mô hình đơn giản cho hệ tụ điện hai lớp có thể được biểu diễn bằng điện dung
tương đương (Cdl), điện trở song song tương đương (Rlk) và điện trở nối tiếp tương
đương (Resr) như hình 2.23.
Hình 2.23: Sơ đồ mạch tương đương của hệ siêu tụ
Một hệ gồm n siêu tụ có dung lượng điện dung (C), giống nhau được mắc nối tiếp,
dung lượng tổng cộng của hệ siêu tụ (Ctotal).
𝐶𝑡𝑜𝑡𝑎𝑙 =
1
1
𝐶1
+
1
𝐶12
+
1
𝐶31
+⋯ . . +
1
𝐶𝑛
=
1
𝑛
𝐶 (2.27)
43
Hiện có hai phương pháp để nạp và xả hệ siêu tụ: một là nạp-xả hệ siêu tụ với điện
áp không đổi theo thời gian, cách còn lại là nạp-xả hệ siêu tụ với cường độ dòng điện
không đổi theo thời gian. Phương pháp nạp và xả hệ siêu tụ dùng điện áp không đổi
được chú trọng và triển khai trong đề tài.
2.5.2 Quá trình nạp của hệ siêu tụ
Hình 2.24 là sơ đồ tương đương quá trình nạp của hệ siêu tụ, được biểu diễn bằng
điện áp nguồn nạp tụ (Vcell), dòng điện phóng của nguồn (Icell), dòng điện nạp hệ siêu
tụ (isc), dòng điện rò (ilk), điện trở rò (Rlk) [25].
Hình 2.24: Sơ đồ tương đương quá trình nạp của hệ siêu tụ
Từ sơ đồ hình 2.24, áp dụng định luật Kirchoff về điện áp:
𝑉𝑐𝑒𝑙𝑙(𝑡) = 𝑉𝑒𝑠𝑟(𝑡) + 𝑉𝑠𝑐(𝑡) (2.28)
= 𝐼𝑐𝑒𝑙𝑙𝑅𝑒𝑠𝑟 + 𝑉𝑠𝑐(𝑡)
Giá trị điện áp trên hệ tụ:
𝑉𝑠𝑐(𝑡) =
1
𝐶𝑡𝑜𝑡𝑎𝑙
∫ 𝑖𝑠𝑐(𝑡)𝑑𝑡 + 𝑉𝑠𝑐
0𝑡
0
(2.29)
Với 𝑉𝑠𝑐
0: giá trị điện áp ban đầu trên hệ siêu tụ.
Từ sơ đồ hình 2.24, áp dụng định luật Kirchoff về dòng điện:
𝑖𝑐𝑒𝑙𝑙(𝑡) = 𝑖𝑙𝑘(𝑡) + ∫ 𝑖𝑠𝑐(𝑡)𝑑𝑡
𝑡
0
(2.30)
Từ (2.28) và (2.30):
𝑉𝑐𝑒𝑙𝑙. 𝐶𝑡𝑜𝑡𝑎𝑙 = 𝑉𝑠𝑐 . 𝐶𝑡𝑜𝑡𝑎𝑙 +∫ 𝑖𝑠𝑐(𝑡)𝑑𝑡
𝑡
0
𝑉𝑐𝑒𝑙𝑙 . 𝐶𝑡𝑜𝑡𝑎𝑙 = 𝑖𝑠𝑐(𝑡). 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 + ∫ 𝑖𝑠𝑐(𝑡)𝑑𝑡
𝑡
0
(2.31)
44
Biến đổi Laplace (2.31):
𝑉𝑐𝑒𝑙𝑙 . 𝐶𝑡𝑜𝑡𝑎𝑙
𝑠
= 𝑖𝑠𝑐(𝑠). 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 +
1
𝑠
𝑖𝑠𝑐(𝑠)
Tương đương
𝑉𝑐𝑒𝑙𝑙 . 𝐶𝑡𝑜𝑡𝑎𝑙 = 𝑖𝑠𝑐(𝑠). 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠 + 𝑖𝑠𝑐(𝑠)
𝑉𝑐𝑒𝑙𝑙 . 𝐶𝑡𝑜𝑡𝑎𝑙 = 𝑖𝑠𝑐(𝑠). (𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠 + 1)
Chia 02 vế cho (𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠 + 1):
𝑖𝑠𝑐(𝑠) =
𝑉𝑐𝑒𝑙𝑙 . 𝐶𝑡𝑜𝑡𝑎𝑙
(𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠 + 1)
Nhân cả tử và mẫu của vế phải với 𝑅𝑙𝑘:
𝑖𝑠𝑐(𝑠) =
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
(𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙.𝑠+1)
×
𝑉𝑐𝑒𝑙𝑙
𝑅𝑙𝑘
(2.32)
Biến đổi
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
(𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙.𝑠+1)
=
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙.(𝑠+
1
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
)
=
1
𝑠+
1
𝑅𝑙𝑘𝐶𝑡𝑜𝑡𝑎𝑙
(2.33)
Thay (2.33) vào (2.32):
𝑖𝑠𝑐(𝑠) =
1
𝑠+
1
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
×
𝑉𝑐𝑒𝑙𝑙
𝑅𝑙𝑘
(2.34)
Trong phép biến đổi ngược Laplace, có:
1
𝑠 − 𝑎
= 𝑒𝑎.𝑡 (với a là hằng số)
Suy ra:
1
𝑠 +
1
𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙
=
1
𝑠 − (−
1
𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙
)
= 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙
Biểu thức (2.34) sau khi biến đổi Laplace ngược:
𝑖𝑠𝑐(𝑡) =
𝑉𝑐𝑒𝑙𝑙
𝑅𝑙𝑘
× 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙 (2.35)
Biểu thức (2.35) mô tả giá trị dòng nạp trên hệ siêu tụ điện trong quá trình nạp.
Thay (2.35) vào (2.29) được điện áp trên tụ.
𝑉𝑠𝑐(𝑡) =
1
𝐶𝑡𝑜𝑡𝑎𝑙
∫
𝑉𝑐𝑒𝑙𝑙
𝑅𝑙𝑘
. 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑑𝑡 + 𝑉𝑠𝑐
0𝑡
0
(2.36)
Biểu thức (2.36) mô tả giá trị điện áp trên hệ siêu tụ điện trong quá trình nạp.
45
2.5.3 Quá trình phóng của hệ siêu tụ
Quá trình phóng của hệ siêu tụ [43] được biểu diễn theo sơ đồ tương đương hình 2.25.
Hình 2.25: Sơ đồ tương đương quá trình phóng của của hệ siêu tụ
Từ sơ đồ hình 2.25, áp dụng định luật Kirchoff về điện áp:
1
𝐶𝑡𝑜𝑡𝑎𝑙
∫ 𝑖𝑠𝑐(𝑡). 𝑑𝑡 + 𝑖𝑠𝑐(𝑡). 𝑅𝑙𝑘 − (𝑉𝑠𝑐
0 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘) = 0
𝑡
0
Nhân 2 vế cho C:
∫𝑖𝑠𝑐(𝑡). 𝑑𝑡 + 𝑖𝑠𝑐(𝑡). 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙 − 𝑉𝑠𝑐
0. 𝐶𝑡𝑜𝑡𝑎𝑙 − 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 = 0
𝑡
0
Biến đổi Laplace:
1
𝑠
𝑖𝑠𝑐(𝑠) + 𝑖𝑠𝑐(𝑠). 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙 −
𝑉𝑠𝑐
0. 𝐶𝑡𝑜𝑡𝑎𝑙
𝑠
−
𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙
𝑠
= 0
𝑖𝑠𝑐(𝑠) + 𝑖𝑠𝑐(𝑠). 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠 = 𝑉𝑠𝑐
0. 𝐶𝑡𝑜𝑡𝑎𝑙 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙
𝑖𝑠𝑐(𝑠). (1 + 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠) = 𝑉𝑠𝑐
0. 𝐶𝑡𝑜𝑡𝑎𝑙 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙
𝑖𝑠𝑐(𝑠) =
𝑉𝑠𝑐
0. 𝐶𝑡𝑜𝑡𝑎𝑙 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙
(1 + 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠)
Nhân cả tử và mẫu với 𝑅𝑙𝑘:
𝑖𝑠𝑐(𝑠) =
(𝑉𝑠𝑐
0 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘). 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙
𝑅𝑙𝑘 . (1 + 𝑅𝑙𝑘. 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠)
𝑖𝑠𝑐(𝑠) =
𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙
(1 + 𝑅𝑙𝑘 . 𝐶𝑡𝑜𝑡𝑎𝑙 . 𝑠)
×
(𝑉𝑠𝑐
0 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘)
𝑅𝑙𝑘
46
Biến đổi ngược Laplace:
𝑖𝑠𝑐(𝑡) =
(𝑉𝑠𝑐
0+𝑖𝑐𝑒𝑙𝑙.𝑅𝑙𝑘)
𝑅𝑙𝑘
× 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙 (2.37)
Mặt khác:
𝑉𝑠𝑐(𝑡) = −
1
𝐶𝑡𝑜𝑡𝑎𝑙
∫ 𝑖𝑠𝑐(𝑡). 𝑑𝑡 + 𝑉𝑠𝑐
0𝑡
0
(2.38)
Thay (2.37) vào (2.38):
𝑉𝑠𝑐(𝑡) = 𝑉𝑠𝑐
0 − (𝑉𝑠𝑐
0 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘). [1 − 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙]
Từ sơ đồ hình 2.27:
𝑉𝑐𝑒𝑙𝑙(𝑡) = 𝑉𝑠𝑐(𝑡) − 𝑉𝑒𝑠𝑟(𝑡)
𝑉𝑐𝑒𝑙𝑙(𝑡) = 𝑉𝑠𝑐
0 − (𝑉𝑠𝑐
0 + 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑙𝑘). [1 − 𝑒
−
𝑡
𝑅𝑙𝑘.𝐶𝑡𝑜𝑡𝑎𝑙] − 𝑖𝑐𝑒𝑙𝑙 . 𝑅𝑒𝑠𝑟 (2.39)
Biểu thức (2.39) mô tả giá trị điện áp trên hệ siêu tụ trong quá trình phóng.
Trong khuôn khổ đề tài, một hệ siêu tụ 27V-35F gồm 10 siêu tụ Maxwell BCAP0350
mắc nối tiếp nhau được sử dụng làm bộ tích trữ năng lượng điện cảm thu hồi từ các
bobine như là một nguồn thứ cấp cung cấp đến kim phun. Hệ số an toàn là 1,125 đảm
bảo hệ siêu tụ hoạt động tốt ở mức điện áp 24V.
Năng lượng cực đại và công suất cực đại mà hệ siêu tụ có thể tích trữ lần lượt được
tính theo biểu thức (2.40) và (2.41) [31]:
𝐸𝑚𝑎𝑥 =
𝐶𝑈2
2𝑥3600𝑥𝑚𝑎𝑠𝑠
(2.40)
𝑃𝑚𝑎𝑥 = 0,06
𝐶𝑈2
𝐸𝑆𝑅𝐷𝐶
(2.41)
Trong đó:
Emax: năng lượng cực đại trên hệ siêu tụ.
Pmax: công suất cực đại trên hệ siêu tụ.
mass: hệ số khối lượng hệ siêu tụ.
ESRDC: điện trở rò hệ siêu tụ.
47
Quá trình chuyển năng lượng từ ắc quy sang hệ siêu tụ và ngược lại sẽ được quyết
định bởi mạch quản lý năng lượng trên ô tô, sẽ đề cập sau ở phần thiết kế mạch quản
lý năng lượng.
2.5.4 Năng lượng trên hệ siêu tụ
Khi hệ siêu tụ được tích điện, hai bản cực của hệ tụ điện tích điện trái dấu nên hình
thành một điện trường hướng từ bản cực dương sang bản cực âm của hệ siêu tụ. Điện
trường này có khả năng sinh ra năng lượng dạng thế năng. Mặt khác, các siêu tụ gồm
n siêu tụ được mắc nối tiếp với nhau tạo thành một hệ siêu tụ có dung lượng tổng
cộng Ctotal. Biểu thức (2.42) biểu thị năng lượng điện trường (Wcap) của hệ siêu tụ với
dung lượng (Ctotal) và điện áp trên tụ (U).
𝑊𝑐𝑎𝑝 =
1
2
𝐶𝑡𝑜𝑡𝑎𝑙𝑈
2 (2.42)
Trong đó điện áp 𝑈 được sử dụng ở mức giá trị 24V để phù hợp với các thiết lập của
thực nghiệm trên mô hình phun xăng đánh lửa và cải thiện tính đáp ứng của kim phun.
Nhằm quản lý hiệu quả nguồn năng lượng trên hệ siêu tụ, cần biết được mức năng
lượng tối đa mà một hệ siêu tụ có thể chứa đựng (biểu thức 2.42), qua đó tính toán
thời gian nạp đầy của hệ siêu tụ dựa vào mức năng lượng từ các xung điện cảm.
Năng lượng từ các xung điện cảm được thu hồi từ quá trình chuyển mạch của các
bobine.
2.5.5 Hệ siêu tụ kết nối phụ tải điện
Việc sử dụng hệ siêu tụ làm nguồn thứ cấp để cung cấp cho và cải thiện độ nhạy của
kim phun là phần thực nghiệm chính trong phạm vi nghiên cứu này. Trong trường
hợp này, tải điện được sử dụng có cấu tạo từ thành phần cuộn cảm. Tải điện dạng
cuộn cảm khác với tải điện dạng điện trở thuần bởi đặc tính của độ tự cảm. Ngoài ra,
cường độ dòng điện trong một mạch kín phụ thuộc vào tải (ở đây là giá trị cảm kháng
của cuộn), người nghiên cứu tiến hành việc mô hình toán hệ siêu tụ với phụ tải điện
dạng điện cảm với mục đích xác định được cường độ dòng điện khi phóng qua tải
điện.
48
Một mạch kín gồm hai thành phần cơ bản là điện dung (C) và độ tự cảm (L). Quá
trình hệ siêu tụ cấp điện đến phụ tải được mô tả bằng một sơ đồ mạch tương đương
ở hình 2.26.
Hình 2.26: Sơ đồ tương đương mạch siêu tụ và phụ tải điện
Tại thời điểm t = 0, trước khi hệ siêu tụ phóng điện, dung lượng, điện áp và cường
độ dòng điện ban đầu của tụ ở trạng thái nạp đầy là Ctotal = C/n và U = U0.
Khi tụ bắt đầu phóng, cường độ dòng điện xuất hiện trong mạch được xác định như
hình 2.26.
Áp dụng định luật Kirchoff về điện áp:
∑𝑈 = 0
𝑈𝑅 + 𝑈𝐿 + 𝑈𝐶 = 0
𝑖𝑅 + 𝐿
𝑑𝐼
𝑑𝑡
+ 𝑈𝐶 = 0 (2.43)
Trong đó:
𝑈𝑅: điện áp trên điện trở.
𝑈𝐿: điện áp trên tải điện là cuộn cảm.
𝑈𝐶: điện áp trên hệ siêu tụ điện.
Trong đó:
𝑈𝑐 = ∫ 𝐼𝑐𝑑𝑡 + 𝑈𝑜 (2.44)
Cường độ dòng điện Ic
𝐼𝑐 = 𝐶𝑡𝑜𝑡𝑎𝑙
𝑑𝑢𝑐
𝑑𝑡
(2.45)
Thay (2.44), (2.45) vào (2.43):
49
𝑅𝐼 +
1
𝐶𝑡𝑜𝑡𝑎𝑙
∫𝐼𝑐𝑑𝑡 + 𝑈𝑜 + 𝐿
𝑑𝐼
𝑑𝑡
= 0
𝑑2𝐼
𝑑𝑡2
+
𝑅
𝐿
𝑑𝐼
𝑑𝑡
+
1
𝐿𝐶𝑡𝑜𝑡𝑎𝑙
𝐼 = 0 (2.46)
Đặt teI , từ (2.46) có:
𝜆2 +
𝑅
𝐿
𝜆 +
1
𝐿𝐶𝑡𝑜𝑡𝑎𝑙
= 0 (2.47)
Phương trình (2.47) là một phương trình bậc hai với hai nghiệm phân biệt.
𝜆 = −
𝑅
2𝐿
± √(
𝑅
2𝐿
)
2
−
1
𝐿𝐶𝑡𝑜𝑡𝑎𝑙
(2.48)
𝐼 = 𝐼0𝑒
−𝑅𝑡
2𝐿 𝑒
√
1
𝐿𝐶𝑡𝑜𝑡𝑎𝑙
−(
𝑅
2𝐿
)
2
𝑡
(2.49)
Phương trình (2.49) là phương trình mô tả cường độ dòng điện trên hình 2.26.
2.6 Tính toán quá trình nạp năng lượng điện cảm vào hệ siêu tụ
2.6.1 Quá trình nạp năng lượng điện cảm trên bobine vào hệ siêu tụ
Trường hợp đơn lẻ một bobine thực hiện quá trình nạp vào siêu tụ, thì số lần (lbb)
bobine thực hiện việc chuyển mạch để có thể nạp đầy được hệ siêu tụ (chưa xét qua
các sai số yếu tố ảnh hưởng bên ngoài như nhiệt độ và môi trường làm việc):
𝑙𝑏𝑏 =
𝑊𝑐𝑎𝑝
𝑊𝑏𝑏
=
1
2
𝑥𝐶𝑡𝑜𝑡𝑎𝑙𝑥𝑈
2
1
2
[
𝑈
𝑅
(1−𝑒
𝑡𝑏𝑏
𝜏 )]
2 =
𝑅2𝐶𝑡𝑜𝑡𝑎𝑙
𝐿(1−𝑒
𝑡𝑏𝑏
𝜏 )
2 (2.50)
Thời gian nạp đầy hệ siêu tụ 𝑡𝑓𝑢𝑙𝑙𝑏𝑏 dựa trên nguồn năng lượng tự cảm của một bobine
tại dải tốc độ động cơ ne:
𝑡𝑓𝑢𝑙𝑙𝑏𝑏 = 𝑙𝑏𝑏
60
𝑛𝑒
(2.51)
Trong đó:
𝑊𝑐𝑎𝑝: năng lượng dự trữ trên hệ siêu tụ (J)
𝑊𝑏𝑏: năng lượng dự trữ trên cuộn sơ cấp (J)
tbb: thời gian transistor công suất điều khiển cuộn sơ cấp dẫn (s)
50
2.6.2 Quá trình nạp năng lượng điện cảm trên kim phun vào hệ siêu tụ
Số lần kim phun thực hiện việc chuyển mạch để có thể nạp đầy hệ siêu tụ:
𝑙𝑘𝑝 =
1
2
𝐶𝑡𝑜𝑡𝑎𝑙𝑥𝑈
2
1
2
[
𝑈
𝑅𝑘𝑝
(1−𝑒
𝑡𝑘𝑝
𝜏 )]
2 =
𝑅𝑘𝑝
2𝐶𝑡𝑜𝑡𝑎𝑙
𝐿𝑘𝑝(1−𝑒
𝑡𝑘𝑝
𝜏 )
2 (2.52)
Thời gian nạp đầy hệ siêu tụ từ năng lượng điện cảm của một kim phun tại tốc độ
động cơ ne:
𝑡𝑓𝑢𝑙𝑙𝑘𝑝 = 𝑙𝑘𝑝
60
𝑛𝑒
(2.53)
Việc tính toán được thời gian nạp của siêu tụ ở các dải động cơ khác nhau bổ trợ cho
việc đánh giá khả năng nạp và thu hồi năng lượng của hệ siêu tụ được trực quan hơn.
2.7 Đặc tính kim phun
2.7.1 Điều khiển kim phun
Hiện nay, các kim phun nhiên liệu trong hệ thống phun xăng được điều khiển theo
hai phương pháp phổ biến, phương pháp điều khiển theo dòng hay còn gọi là phương
pháp “nhấc và giữ” (Peak and Hold) và phương pháp điều khiển theo áp (Saturated
Voltage). Trong quá trình chuyển mạch, cuộn cảm trong kim phun tạo ra một suất
điện động ngược về phía nguồn cấp cho kim phun, điều này vẫn là một trong những
nhược điểm cố hữu của các bộ chấp hành có cấu tạo từ cuộn cảm.
Hình 2.27: Điện áp ở hai chế độ điều khiển kim phun
Cả hai phương pháp điều khiển như trên đều cấp một nguồn điện áp đến kim phun để
nhấc kim. Tuy nhiên, ở phương pháp điều khiển theo dòng, mạch điều khiển sẽ cấp
dòng điện có cường độ cao để mở kim phun, sau đó dòng điện sẽ được giảm xuống
51
bằng cách hạ điện áp xuống đủ để duy trì hoạt động mở của kim với mục đích làm
giảm một phần suất điện động khi chuyển mạch (hình 2.27). Với cùng một điện áp
cung cấp ở cả hai phương pháp, ở chế độ điều khiển theo dòng, việc nhấc và giữ kim
yêu cầu kim phun có trở kháng thấp hơn so với phương pháp điều khiển theo áp. Tuy
nhiên, nếu xét về phương diện thu hồi năng lượng điện cảm, kim phun được điều
khiển theo áp sẽ có lợi hơn do suất điện động tự cảm ở chế độ điều khiển này có biên
độ lớn hơn so với chế độ điều khiển theo dòng.
2.7.2 Phân tích quá trình hoạt động của kim phun
Kim phun xăng được cấu thành từ 09 bộ phận như hình 2.28.
Hình 2.28: Cấu tạo của kim phun [26]
1 – nhiên liệu; 2 – lọc nhiên liệu; 3 – giắc nối điện; 4 – vỏ kim phun; 5 – cuộn từ;
6 – ty kim; 7 – lỗ phun; 8 – tia phun; 9 – lò xo hồi vị
2.7.3. Mô hình toán của kim phun
Lưu lượng nhiên liệu phun qua lỗ phun phụ thuộc vào áp suất nhiên liệu và thời gian
nhấc kim. Khoảng thay đổi của áp suất nhiên liệu được xác định qua biểu thức 2.54
[27]:
∆𝑃 =
∆𝑉
𝑉
(2.54)
Trong đó:
𝑃: áp suất nhiên liệu
𝑉: thể tích nhiên liệu phun qua kim
52
∆𝑃: phần áp suất thay đổi
∆𝑉: phần thể tích thay đổi
Lưu lượng nhiên liệu vào và ra được được mô tả theo phương trình Bernoulli:
𝑄 = 𝜇𝐴√
2∆𝑃
𝜌
(2.55)
Trong đó:
𝜇: độ nhớt nhiên liệu
𝐴: tiết diện đầu ty kim
𝜌: khối lượng riêng nhiên liệu
Từ biểu thức 2.54 và 2.55: sự thay đổi áp suất trên thể tích chứa nhiên liệu được mô
tả theo biểu thức 2.56:
𝑑𝑃
𝑑𝑡
= [∑𝑄𝑖𝑛 + 𝑄𝑙𝑒𝑎𝑘𝑖𝑛 − 𝑄𝑜𝑢𝑡 − 𝑄𝑙𝑒𝑎𝑘𝑜𝑢𝑡 + ∑𝐴
𝑑𝑥
𝑑𝑡
]
𝐸
𝑉
(2.56)
Trong đó:
𝑄𝑖𝑛 : lưu lượng nhiên liệu vào
𝑄𝑜𝑢𝑡: lưu lượng nhiên liệu ra
𝑄𝑙𝑒𝑎𝑘𝑖𝑛: lưu lượng nhiên liệu rò trong quá trình vào
𝑄𝑙𝑒𝑎𝑘𝑜𝑢𝑡: lưu lượng nhiên liệu rò trong quá trình ra
𝑥: khoảng dịch chuyển của ty kim
Chuyển động của ty kim được biểu diễn qua phương trình động lực học 2.57:
𝑚
𝑑2𝑥
𝑑𝑡2
+ 𝜉
𝑑𝑥
𝑑𝑡
+ 𝑘𝑥 = ∑𝐹𝑠 + ∑𝐹𝑓 + ∑𝐹𝑚 (2.57)
Trong đó:
𝐹𝑠: lực lò xo hồi vị
𝐹𝑓: áp lực nhiên liệu
𝐹𝑚: lực từ
𝑚: là khối lượng ty kim
53
𝜉: hệ số dao động tắt dần
Chuyển động của ty kim là hoạt động quan trọng của kim phun. Chuyển động này
được phân tích thông qua bốn thành phần tử: phần tử điện, phần tử điện từ, phần tử
cơ khí và phần tử thủy lực như hình 2.29.
Phần tử
điện
Phần tử
điện từ
Phần tử
cơ khí
𝐹𝑓
Phần tử
thủy lực
𝑉 𝑖 𝐹𝑚
𝑅 𝑥 𝑥
≠ 1 𝑑𝜑
𝑑𝑡
𝑑𝑥
𝑑𝑡
𝑑𝑥
𝑑𝑡
𝑑2𝑥
𝑑𝑡2
Hình 2.29: Mô hình hệ điện – điện từ - cơ - thủy lực của kim phun
Hệ phương trình mô hình hóa kim phun trong hệ bốn phần tử: điện - điện từ - cơ khí
- thủy lực:
{
(𝐿𝑠 + 𝐿𝑎)
𝑑𝑖
𝑑𝑡
+ (𝑅𝑠 + 𝑅𝑎 + 𝑅𝐿)𝑖 + 𝑉𝑐 = 𝑉0
𝑖 = 𝐶
𝑑𝑉𝑐
𝑑𝑡
𝑑2𝑥
𝑑𝑡2
=
1
𝑚
𝐹𝑚 −
1
𝑚
𝑘(𝑥 + 𝑥0) −
1
𝑚
𝐹𝑓 −
1
𝑚
𝜉
𝑑𝑥
𝑑𝑡
(2.58)
{
𝐹𝑚 =
𝜇0(𝑁𝑖)
2𝑆𝑎
2(𝛿−𝑥)2
𝐹𝑓 = 𝑓(𝑥,
𝑑𝑥
𝑑𝑡
, 𝑃𝑐𝑜𝑛, 𝑃𝑏𝑝𝑎)
(2.59)
Trong đó:
𝐿𝑠: độ tự cảm lúc ban đầu.
𝐿𝑎: độ tự cảm lúc sau của cuộn từ.
𝑖: dòng điện qua cuộn dây.
𝑅𝑠: điện trở lúc ban đầu.
𝑅𝑎: điện trở lúc sau của cuộn dây điện từ.
54
𝑅𝐿: điện trở giới hạn dòng điện cực đại.
𝑉0: điện áp ban đầu cung cấp đến cuộn dây điện từ.
𝑉𝑐: điện áp nạp tụ.
𝐶𝑝: điện dung tụ.
𝐹𝑚: lực từ.
𝜇0: độ từ thẩm trong chân không.
𝑁𝑖: số vòng quấn trên cuộn dây.
𝑆𝑎: từ thông qua tiết diện mặt cắt ngang.
𝛿: khoảng cách ban đầu.
𝑃𝑐𝑜𝑛: áp suất điều khiển.
𝑃𝑏𝑝𝑎: áp suất nhiên liệu hồi.
2.7.4 Đặc tính cường độ dòng điện qua kim phun
Khi điện áp cấp đến kim phun, dòng điện trong cuộn từ sẽ tăng dần do sự cản trở của
dòng tự cảm, dòng điện sinh ra có xu hướng chống lại nguyên nhân sinh ra nó, một
đặc tính cơ bản của cuộn dây. Dòng điện tăng dần tương ứng với lực từ tác dụng lên
ty kim tăng dần, đến thời điểm nhất định, khi lực từ lớn hơn lực nén của lò xo hồi vị
và áp lực từ nhiên liệu, ty kim sẽ dịch chuyển lên trên và nhiên liệu được phun vào
xy lanh.
Hình 2.30: Đặc tính, độ tự cảm cường độ dòng điện qua kim phun [28]
55
Trên hình 2.30, khi kim phun được cấp điện, cường độ dòng điện trong cuộn từ bắt
đầu tăng từ 0A đến khi lực điện từ lớn hơn áp lực tổng cộng đặt vào đầu kim, ty kim
sẽ được nhấc lên. Lúc này, cường độ dòng điện qua kim phun sẽ có khoảng rơi nhỏ
do suất điện động tự cảm trong cuộn tăng lên do L tăng [28]. Sau đó cường độ dòng
điện trong kim tiếp tục tăng cho đến khi đạt giá trị bão hòa, giá trị này tuân theo định
luật Ohm dựa trên điện trở và điện áp đặt vào kim.
Mối quan hệ giữa các đường đặc tính điện áp, cường độ dòng điện có quan hệ theo
biểu thức 2.60.
𝐼 =
𝑈
𝑅
(1 − 𝑒
−𝑅
𝐿
𝑡) (2.60)
Trong đó, U là điện áp cung cấp, R và L lần lượt là giá trị điện trở và độ tự cảm của
kim phun.
Gọi thời gian T1 – dead time hay thời gian chết được tính từ lúc dòng điện tăng từ 0
đến Icr (hình 2.30). Khi dòng điện cuộn dây tăng đến Icr, lực điện từ lúc này lớn hơn
sự chênh lệch lực tác dụng giữa lực nén của lò xo hồi vị và áp suất nhiên liệu, ty kim
bắt đầu chuyển động lên, tương ứng với giai đoạn bắt đầu T2, đến hết giai đoạn T2 là
lúc ty kim được nhấc lên hoàn toàn khỏi bệ. Giai đoạn tiếp theo T3, dòng điện qua
kim phun vẫn tiếp tục tăng cho đến khi đạt giá trị bão hòa. Cuối cùng, ở giai đoạn T4,
dòng điện không tăng nữa, giữ ở mức bão hòa. Trong khoảng thời gian T2 + T3, kim
phun dịch chuyển làm lượng nhiên liệu phun thiếu chính xác.
Gọi L và L’ lần lượt là độ tự cảm của kim phun ở giai đoạn trước và sau khi nhấc kim.
Khi L’> L, giá trị độ tự cảm tăng hoặc giảm theo quy luật của hàm mũ.
𝐿′ =
𝐿
𝑒−𝑡
(2.61)
∆𝐿 = 𝐿′ − 𝐿 = 𝐿′(1 − 𝑒−𝑡) (2.62)
Quá trình thay đổi của độ tự cảm L trong kim phun ở quá trình nhấc kim thành 3 giai
đoạn như hình 2.30.
Quá trình thay đổi cường độ dòng điện qua kim phun được biểu diễn qua 04 giai
đoạn:
56
Giai đoạn 1 (T1): ty kim đóng, độ tự cảm lúc này có giá trị là L1
Ở giai đoạn này, cường độ dòng điện tăng lên tương ứng với khoảng thời gian T1 trên
hình 2.30. Lúc này, lực từ (Fm) trong kim phun là rất nhỏ so với cản lực tổng cộng
của lò xo hồi vị (Fs) và của áp lực nhiên liệu (Ff).
𝐹𝑓 + 𝐹𝑠 ≫ 𝐹𝑚 (2.63)
Cường độ dòng điện trong giai đoạn 1:
𝐼1 =
𝑈
𝑅
(1 − 𝑒
−𝑅
𝐿
𝑡1) (2.64)
Giai đoạn 2 (T2): ty kim bắt đầu nhấc lên, độ tự cảm lúc này sẽ tăng từ L lên L’
Trong giai đoạn này, lực từ đã thắng được các trở lực, ty kim bắt đầu nhấc lên khỏi
bệ.
𝐹𝑓 + 𝐹𝑠 = 𝐹𝑚 (2.65)
Mặt khác, độ tự cảm của kim phun bắt đầu tăng lên từ L →L’, cường độ dòng điện
lúc này sẽ giảm xuống đột ngột (dI/dt khác 0).
𝐼2 =
𝑈
𝑅
(1 − 𝑒
−𝑅
∆𝐿
𝑡2) =
𝑈
𝑅
(1 − 𝑒
−𝑅
𝐿′−𝐿
𝑡2) =
𝑈
𝑅
(1 − 𝑒
−𝑅
𝐿′(1−𝑒−𝑡)
𝑡2) (2.66)
Từ biểu thức 2.66, nhận thấy U, R các là giá trị không đổi trong quá trình nhấc kim,
nên độ tự cảm tăng lên đột ngột dẫn đến cường độ dòng điện sẽ giảm xuống. Tuy
nhiên, khoảng thời gian cường độ dòng điện rơi xuống là rất ngắn, vì giá trị t2 tăng
dần theo thời gian, dẫn đến )(' 2te1L tiến dần đến L’, lúc này cường độ dòng điện sẽ
tiếp tục tăng lên.
Giai đoạn 3 (T3): ty kim được nhấc lên hoàn toàn, độ tự cảm có giá trị là L’
Trong giai đoạn này, lực từ đã lớn hơn cản lực của lò xo và cản lực của nhiên liệu.
Ty kim đã được nhấc lên hoàn toàn khỏi bệ.
𝐹𝑓 + 𝐹𝑠 < 𝐹𝑚 (2.67)
Lúc này độ tự cảm đã đạt giá trị L’, cường độ dòng điện tiếp tục tăng dần cho đến khi
đạtFile đính kèm:
 luan_an_nghien_cuu_ung_dung_nang_luong_dien_cam_tren_o_to.pdf
luan_an_nghien_cuu_ung_dung_nang_luong_dien_cam_tren_o_to.pdf 7. Trang thông tin luan an Tiếng Anh _ Phan Nguyen Qui Tam 08-06- 02021.docx
7. Trang thông tin luan an Tiếng Anh _ Phan Nguyen Qui Tam 08-06- 02021.docx 6. Trang thông tin luan an Tiếng Việt _ Phan Nguyen Qui Tam 08-06- 02021.docx
6. Trang thông tin luan an Tiếng Việt _ Phan Nguyen Qui Tam 08-06- 02021.docx 3. Tom tat luan tieng Anh_ Phan Nguyen Qui Tam 08-06-2021.pdf
3. Tom tat luan tieng Anh_ Phan Nguyen Qui Tam 08-06-2021.pdf 2. Tom tat luan an tieng Viet _Phan Nguyen Qui Tam 08-06-2021.pdf
2. Tom tat luan an tieng Viet _Phan Nguyen Qui Tam 08-06-2021.pdf

