Luận án Ước lượng và điều khiển tối ưu trạng thái pin lithium-ion ứng dụng cho hệ thống bms

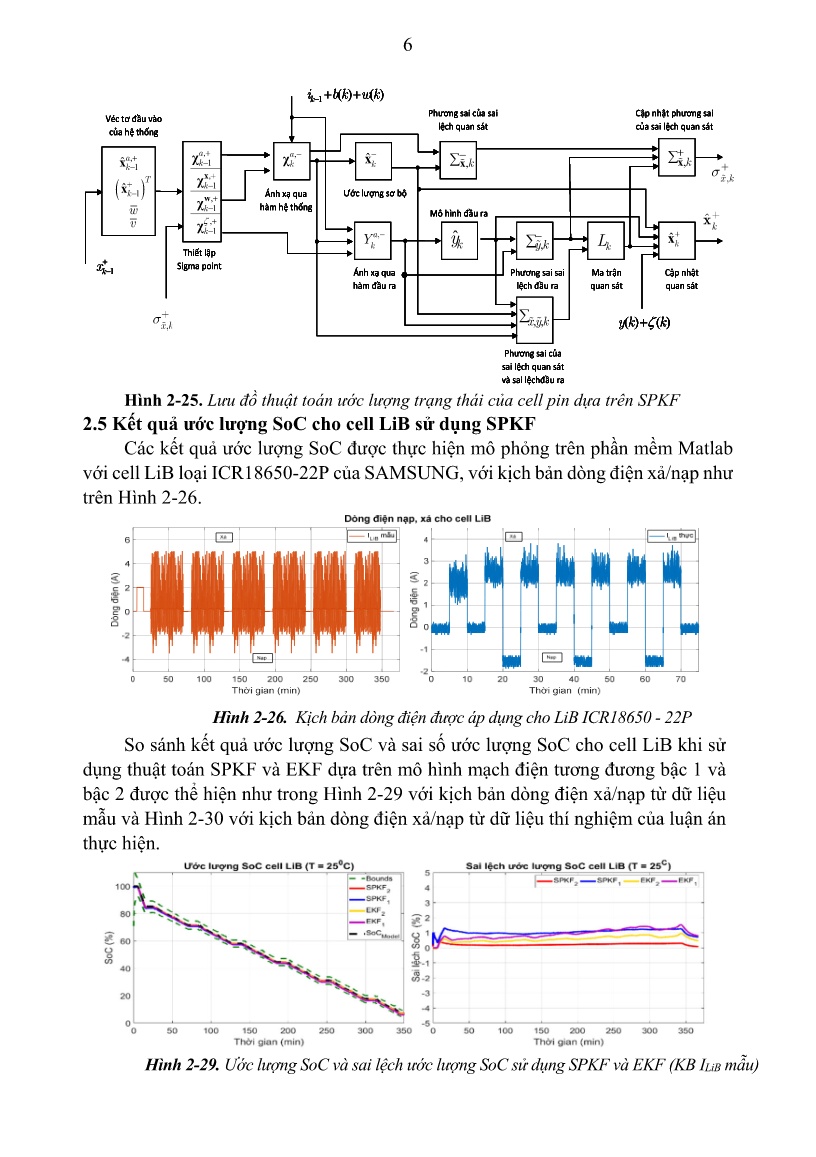
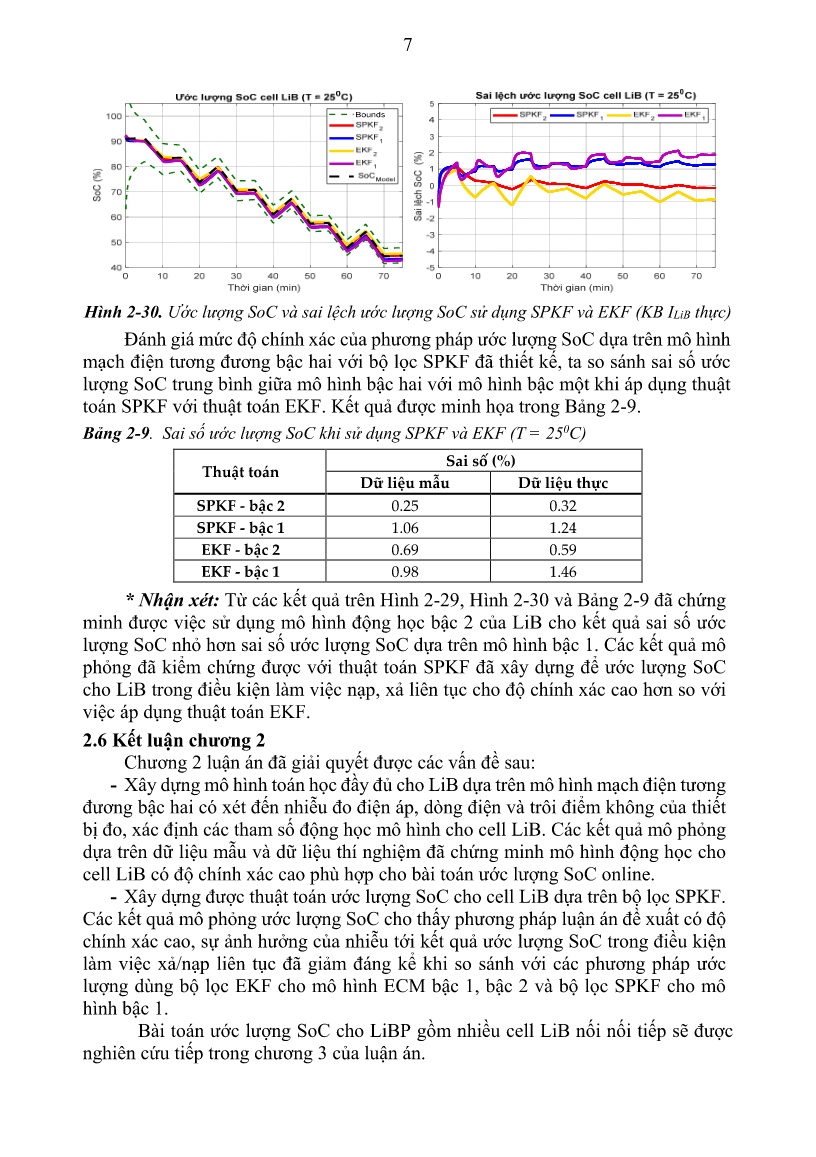
 0 ux (2.19) 
Phương trình điện áp đầu ra: 
( ) 0 0
2
1
 ( ) ( )( ) ( ), ( () )
=
+ −+= −∑ ii Rk
i
y k OCV z k T Mh R iM s Rk ik kk (2.20) 
Đặt các ma trận hệ thống ( ( ))A i k , ( ( ))B i k và các ma trận đầu ra ( )C k , ( )D k : 
1 2
2 1 2 1
( )
0
1 0
 0 ,) 
0 0 0 1
( ( ) ( ( ))
( ) ( )
k
RC RC
S
H H
T
i k i k
A
k
Q
A B
Ak k
η
×
× ×
 −  
  
  
   −  
 
=

=A
0
0 0B (2.21) 
[ ]1 2 0( ) 0 , ( ) [ 0]k R R M k R= − − = −C D (2.22) 
Mô hình toán học của LiB biểu diễn bằng mô hình mạch điện tương đương bậc 2: 
( )
( 1) ( ( )) ( ) ( ( )) ( )
 ( ) ( ) ( ) (( ) ( )) ( ),
x A x B
C D Ex x kT
k i k k i k u k
k k k u ky k OCV k k
+ = +
 + + =
 (2.23) 
Trong phương trình (2.23), mối quan hệ giữa OCV và SoC là mối quan hệ phi tuyến, 
các ma trận ( ( ))A i k và ( ( ))B i k phụ thuộc các tham số đầu vào của mô hình là dòng 
điện i(k) và các tham số ( )0 1 1 2 2 0, , , , , , ,, , , ( )η γ kR OCV zR C M kR C TM , các ma 
trận trong (2.23) đều phụ thuộc vào nhiệt độ của LiB. 
2.3 Xác định các tham số của mô hình cell LiB 
2.3.1 Xác định quan hệ giữa OCV và SoC 
2.3.2 Xác định hiệu suất Coulomb 
2.3.3 Xác định quan hệ giữa OCV và SoC theo nhiệt độ 
2.3.4 Xác định các tham số còn lại của mô hình động học 
2.3.5 Kết quả xác định các tham số của mô hình một loại cell LiB 
2.4 Ước lượng SoC cho cell pin LiB sử dụng bộ lọc SPKF 
2.4.1 Thuật toán SPKF trong bài toán ước lượng trạng thái hệ phi tuyến 
2.4.2 Ước lượng SoC cho cell LiB sử dụng SPKF dựa trên mô hình mạch điện tương 
đương bậc 2 
Thuật toán ước lượng vectơ trạng thái x(k) sử dụng SPKF dựa trên mô hình 
mạch điện tương đương bậc 2 tại thời điểm lấy mẫu k được thực hiện theo hai bước: 
- Bước 1: Xác định đầu ra ước lượng của hệ tại thời điểm lấy mẫu k 
- Bước 2: Hiệu chỉnh ước lượng đầu ra của hệ 
Lưu đồ thuật toán ước lượng véc tơ trạng thái x(k) sử dụng SPKF dựa trên mô 
hình cell bậc 2 tại thời điểm lấy mẫu k được mô tả trên Hình 2-25. 
6 
Hình 2-25. Lưu đồ thuật toán ước lượng trạng thái của cell pin dựa trên SPKF 
2.5 Kết quả ước lượng SoC cho cell LiB sử dụng SPKF 
 Các kết quả ước lượng SoC được thực hiện mô phỏng trên phần mềm Matlab 
với cell LiB loại ICR18650-22P của SAMSUNG, với kịch bản dòng điện xả/nạp như 
trên Hình 2-26. 
Hình 2-26. Kịch bản dòng điện được áp dụng cho LiB ICR18650 - 22P 
So sánh kết quả ước lượng SoC và sai số ước lượng SoC cho cell LiB khi sử 
dụng thuật toán SPKF và EKF dựa trên mô hình mạch điện tương đương bậc 1 và 
bậc 2 được thể hiện như trong Hình 2-29 với kịch bản dòng điện xả/nạp từ dữ liệu 
mẫu và Hình 2-30 với kịch bản dòng điện xả/nạp từ dữ liệu thí nghiệm của luận án 
thực hiện. 
Hình 2-29. Ước lượng SoC và sai lệch ước lượng SoC sử dụng SPKF và EKF (KB ILiB mẫu) 
,
1
a
k
+
−χ 
,
1k
+
−
xχ 
,
1k
+
−
wχ 
,
1k
ζ +
−χ 
,−χak 
−a
k
Y , 
ˆ
k
−x 
kˆy 
,
−∑xɶ k
,
−∑ɶy k kL ˆ
+xk 
,
+∑xɶ k, 1ˆ
a
k
+
−x 
( )1ˆ
T
k
+
−x 
w 
v 
1 ( ) ( )− + +ki b k w k 
, ,∑ ɶɶx yk ( ) ( )ζ+y k k 
Ma trận 
quan sát 
Phương sai của 
sai lệch quan sát 
và sai lệchđầu ra 
Cập nhật 
quan sát 
kx 
Cập nhật phương sai 
của sai lệch quan sát 
Ánh xạ qua 
hàm đầu ra 
Ánh xạ qua 
hàm hệ thống 
Phương sai của sai 
lệch quan sát 
Thiết lập 
Sigma point 
, 1
+
−∑ɶx k 
1
+
−kx 
Véc tơ đầu vào 
của hệ thống 
Ước lượng sơ bộ 
Phương sai sai 
lệch đầu ra 
Mô hình đầu ra 
ζ 
x k, 1
σ+
−ɶ 
x k,
σ
ɶ x k,
σ+
ɶ
y ,
σ
ɶ
xy k,
σ
ɶɶ 
x k,
σ+
ɶ
k
ˆ+x 
7 
Hình 2-30. Ước lượng SoC và sai lệch ước lượng SoC sử dụng SPKF và EKF (KB ILiB thực) 
Đánh giá mức độ chính xác của phương pháp ước lượng SoC dựa trên mô hình 
mạch điện tương đương bậc hai với bộ lọc SPKF đã thiết kế, ta so sánh sai số ước 
lượng SoC trung bình giữa mô hình bậc hai với mô hình bậc một khi áp dụng thuật 
toán SPKF với thuật toán EKF. Kết quả được minh họa trong Bảng 2-9. 
Bảng 2-9. Sai số ước lượng SoC khi sử dụng SPKF và EKF (T = 250C) 
Thuật toán 
Sai số (%) 
Dữ liệu mẫu Dữ liệu thực 
SPKF - bậc 2 0.25 0.32 
SPKF - bậc 1 1.06 1.24 
EKF - bậc 2 0.69 0.59 
EKF - bậc 1 0.98 1.46 
* Nhận xét: Từ các kết quả trên Hình 2-29, Hình 2-30 và Bảng 2-9 đã chứng 
minh được việc sử dụng mô hình động học bậc 2 của LiB cho kết quả sai số ước 
lượng SoC nhỏ hơn sai số ước lượng SoC dựa trên mô hình bậc 1. Các kết quả mô 
phỏng đã kiểm chứng được với thuật toán SPKF đã xây dựng để ước lượng SoC 
cho LiB trong điều kiện làm việc nạp, xả liên tục cho độ chính xác cao hơn so với 
việc áp dụng thuật toán EKF. 
2.6 Kết luận chương 2 
 Chương 2 luận án đã giải quyết được các vấn đề sau: 
- Xây dựng mô hình toán học đầy đủ cho LiB dựa trên mô hình mạch điện tương 
đương bậc hai có xét đến nhiễu đo điện áp, dòng điện và trôi điểm không của thiết 
bị đo, xác định các tham số động học mô hình cho cell LiB. Các kết quả mô phỏng 
dựa trên dữ liệu mẫu và dữ liệu thí nghiệm đã chứng minh mô hình động học cho 
cell LiB có độ chính xác cao phù hợp cho bài toán ước lượng SoC online. 
- Xây dựng được thuật toán ước lượng SoC cho cell LiB dựa trên bộ lọc SPKF. 
Các kết quả mô phỏng ước lượng SoC cho thấy phương pháp luận án đề xuất có độ 
chính xác cao, sự ảnh hưởng của nhiễu tới kết quả ước lượng SoC trong điều kiện 
làm việc xả/nạp liên tục đã giảm đáng kể khi so sánh với các phương pháp ước 
lượng dùng bộ lọc EKF cho mô hình ECM bậc 1, bậc 2 và bộ lọc SPKF cho mô 
hình bậc 1. 
Bài toán ước lượng SoC cho LiBP gồm nhiều cell LiB nối nối tiếp sẽ được 
nghiên cứu tiếp trong chương 3 của luận án. 
8 
Chương 3. ƯỚC LƯỢNG SoC CHO LiBP SỬ DỤNG BỘ LỌC SPKF 
3.1 Đặt vấn đề 
3.2 Mô hình động học của cell LiB khi xét đến trôi điểm không của phép đo 
dòng điện và mô hình của LiBP 
3.2.1 Mô hình ECM bậc 2 của LiB có xét đến nhiễu đo điện áp, nhiễu và trôi điểm 
không dòng điện. 
Gọi độ trôi điểm không của phép đo dòng điện qua cell là b(t), dựa trên mô 
hình của cell đã xây dựng ở mục 2.2.3, ta đưa thêm b(t) vào mô hình để ước lượng 
trôi điểm không. Khi đó véc tơ các biến trạng thái khi đó sẽ gồm 5 biến như sau: 
1 1
( ) ( ) ( ) ( ) ( ) ( )x
T
R Rk z k i k i k h k b k =   (3.1) 
Mô hình trạng thái của cell khi đó được viết là: 
k i k k i k k k( 1) ( ( )) ( ) ( ( )) ( ) ( )+ = + +x A x B u w (3.2) 
Các ma trận trong phương trình (3.2) có dạng: 
1 1
2 2
1 1 2 2 1 1 1 1 2 2 2 2
1 1 2 2
0 0 0 0
0 0 0 0
( ( )) , ( ( ))0 0 0 0
sgn( )
0 0 0 1 0
0 0 0 0 1
exp , exp , 1 , 1 ,
exp
 
 
 
      = =        
 
 
 
   −∆ −∆    = = = − = −        
 ∆= −

A B
RC
R C
k
h
k
R C R C RC RC R C R C
k k k
h
A
A
i
i k i kA
i
t t
A A B A B A
RC RC
i t
A
Q
η γ
1 2 3 4 5
; 1 , ( ) ( ) ( ) ( ) ( ) ( )
   = − =      
w
T
h h
B A k w k w k w k w k w k
(3.3) 
Phương trình đầu ra của mô hình cell LiB: 
( ) )( ) ( ), ( ) ( ( ) ( ) ( )C x D ζ+ += +ky k kk OCV kz ik k kT (3.4) 
Mô hình bậc 2 của cell LiB có xét đến trôi điểm không, nhiễu đo dòng điện và 
nhiễu đo điện áp của cell: 
( )
( 1) ( ( )) ( ) ( ( )) ( ) ( )
( ) ( )( ) ( ,) ( ) ( () ( ))
x A x B u w
C x D E xy k OCV k k T
k i k k i k k k
k k k i k kk=
+ = + +

+ + + ζ 
(3.5) 
3.2.2 Mô hình của LiBP 
Giả thiết một LiBP bao gồm NS mô đun mắc nối tiếp, mỗi mô đun gồm NP cell 
LiB mắc song song. Định nghĩa các tham số mô tả cho một LiBP như sau 
( )
o 0S C
×
∈ s p
N N
R là ma trận biểu diễn SoC0 ban đầu của các cell, 
( )
0R
×
∈ s p
N N
R 
là ma trận biểu diễn điện trở trong R0,
( )
0Q
×
∈ s p
N N
R là ma trận biểu diễn dung 
lượng của các cell. 
- SoC ban đầu (tại thời điểm k = 0) của mô đun thứ i: 
1
( , ), 1,2,...,00,
1
SoC = =
=
∑
Np
mz i j i Nsi Np j
 (3.6) 
9 
- Điện trở trong R0 của mô đun thứ i được xác định: 
1
 1,2,...,0, 1
1 ( , )0R
= =
=∑
p
R i Ni sN
j i j
 (3.7) 
- Dung lượng của mô đun thứ i trong LiBP: 
( , ) 1,2,...,0, 01Q= ==∑
pNQ i j i Ni sj (3.8) 
3.3 Ước lượng SoC cho LiBP sử dụng bộ lọc SPKF 
Quá trình ước lượng được tiến hành qua hai bước tại mỗi thời điểm trích mẫu k: 
* Bước 1: Ước lượng SoC trung bình của NS mô đun và trôi điểm không của 
dòng điện qua LiBP, bước này thực hiện bằng thuật toán SPKF1 
* Bước 2: Ước lượng độ lệch SoC của từng mô đun so với SoC trung bình đã xác 
định ở bước 1, sau đó ước lượng SoC cho từng mô đun bằng tổng của SoC trung bình 
cộng với độ lệch SoC tương ứng của từng mô đun, thực hiện bằng thuật toán SPKF2. 
3.3.1 Thuật toán tổng quát ước lượng SoC của LiBP 
3.3.2 Thuật toán ước lượng SoC trung bình của cả LiBP 
- Thiết lập véc tơ trạng thái phụ tại thời điểm lấy mẫu k 
,ˆ ˆ , ,-1 -1
T
a Tx x w
k k
ζ+ + =   
 (3.10) 
- Thiết lập ma trận hiệp phương sai phụ của sai lệch ước lượng véc tơ trạng thái: 
( ), , ,, 1 , 1ɶ ɶa diag wx k x kσ σ σζ+ +Σ =− − (3.11) 
- Tạo véc tơ điểm Sigma đầu vào gồm p+1 điểm Sigma: 
,, , , , , , , ,ˆ ˆ ˆ, , , ,1 1 1 , 1 1 , 1 1 1 1ɶ ɶ
T
a a a a a a x wX x x x X X X
k k k x k k x k k k k
ζγ γ  ++ + + + + + + + = + ∑ − ∑ = − − − − − − − − −   
 (3.12) 
- Tính toán ma trận điểm Sigma trạng thái tại thời điểm k: 
( ), , , , ,, ,, 1 1 1 1x x w x wX f X i X A X B u Xk k k kk j k k k k− + + + += = + +− − − −
(3.13)
- Ước lượng sơ bộ véc tơ trạng thái tại thời điểm k: 
,ˆ ,
0
p
xmx X ak j k j
j
α −− =
=
∑
(3.14)
- Cập nhật ma trận hiệp phương sai của sai lệch ước lượng biến trạng thái: 
( ) ( ), ,ˆ ˆ, , ,
0
ɶ
p T
x xc X x X xx k k kj k j k j
j
α − −− − −Σ = − −
=
∑
(3.15)
- Tính ma trận điểm Sigma đầu ra tại thời điểm k: 
 ( ) ,,-ˆ , -1
x
Y OCV z C X D u Xk k k k kk j k
ζ += + + +
(3.16) 
- Ước lượng đầu ra điện áp của LiBP: 
10 
ˆ
0
p
my Yk kj
j
α=
=
∑ (3.17)
- Cập nhật ma trận hiệp phương sai của sai lệch ước lượng đầu ra: 
( )( )ˆ ˆ,
0
ɶ
p
Tc Y y Y yy k k k k kj
j
α∑ = − −
=
∑ (3.18) 
- Cập nhật ma trận hiệp phương sai tương quan giữa sai lệch ước lượng biến 
trạng thái và sai lệch điện áp đầu ra: 
( ) ( ), ˆˆ, , ,
0
ɶɶ
p
Txc X x Y yx y k k k kj k j
j
α −− −∑ = − −
=
∑ (3.19)
- Tính toán cập nhật ma trận ước lượng trạng thái: 
, ,
,
ɶɶ
ɶ
x y k
Lk
y k
−∑
=
∑
 (3.20) 
- Cập nhật trạng thái ước lượng của cell tương đương bằng cách tính toán các 
sai số đầu ra, ước lượng của véc tơ trạng thái là: 
( )ˆˆ ˆx x L y yk k k kk
+ −= + −
(3.21) 
- Cập nhật ma trận hiệp phương sai của sai lệch ước lượng trạng thái: 
, ,, ɶɶɶ
TL Lx k k y k kx k
+ −∑ = ∑ − ∑
(3.22)
 3.3.3 Thuật toán ước lượng SoC của các mô đun 
Mô hình dùng để ước lượng độ lệch SoC, với 
k k b k
I i i
,
ˆ= − 
( )
i i
k k k si
i i i i i i i
k k k k k k R k R k k
z z I i N
Q
u OCV z z T I R Mh R C i R C i R I
1 2
( ) ( )
1 ( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
1 1 1 , 2 2 , 0
1
, 1, 2,...,
3600
ˆ ,
+
+
∆ = ∆ − =
 = +∆ − ∆ + − − −
 (3.23) 
 Thuật toán ước lượng SoC các mô đun được thực hiện như sau: 
 - Thiết lập véc tơ trạng thái phụ của mô đun i, thiết lập ma trận hiệp phương sai 
phụ của sai lệch ước lượng độ lệch SoC của mô đun i, tạo ma trận điểm Sigma đầu 
vào của mô đun thứ i. Tính ma trận điểm Sigma trạng thái của mô đun i 
- Ước lượng độ lệch SoC của mô đun thứ i tại thời điểm k: 
 ,( )( )ˆ ,
0
α χ∆ −−∆ = ∆
=
∑
p
z ii mzk j k j
j
 (3.28) 
- Ước lượng điện áp đầu ra của mô đun thứ i: 
 ( ) ( )ˆ
0
α=
=
∑
p
i imu Ujk k
j
 (3.31) 
- Cập nhật ma trận ước lượng trạng thái của mô đun thứ i: 
11 
( )
, ,( )
( )
,
ɶɶ
ɶ
i
z u ki
L
k i
u k
σ
σ
−
∆= (3.34) 
- Độ lệch SoC của mô đun thứ i là: 
 ( ) ( )( ) ( ) ˆ ˆˆ ˆ+ −  ∆ = ∆ + − 
 
i ii iz z L u uk kk k k (3.35) 
- Cập nhật ma trận hiệp phương sai sai lệch ước lượng độ lệch SoC mô đun thứ i: 
( ) ( ) ( ) ( ) ( )
, , ,ɶɶ ɶ
Ti i i i i
z k z k k u k kL Lσ σ σ
+ −
∆ ∆= − (3.36) 
3.3.4 Các kết quả ước lượng SoC cho LiBP 
Từ thí nghiệm ta xác định được các tham số mô hình động học của cell LiB theo nhiệt 
độ, SoC ban đầu, điện trở R0 và dung lượng ban đầu của các cell trong LiBP với kịch 
bản dòng xả/nạp qua LiBP như hình 3-7 
Hình 3-7. Dòng điện qua LiBP với kịch bản nạp - xả có biên độ thay đổi 
Các kết quả ước lượng SoC của các mô đun trong LiBP được thể hiện trên Hình 
3-11, Hình 3-13 và Hình 3-14. 
Hình 3-11. Kết quả ước lượng SoC của các mô đun trong LiBP 
Thời gian (min) 
Dòng điện của LiBP 
D
ò
n
g
 đ
iệ
n
 (
A
) 
Thời gian (min) 
Thời gian (min) 
12 
Hình 3-13. Ước lượng độ trôi điểm không của dòng điện qua LiBP 
Hình 3-14. So sánh sai số ước lượng SoC của các mô đun trong LiBP theo nhiệt độ 
3.4 Kết luận chương 3 
 Chương 3 luận án đã giải quyết được các vấn đề sau: 
- Đã xây dựng mô hình động học cho LiB và LiBP dựa trên mô hình mạch điện 
tương đương bậc 2 của cell có xét đến trôi điểm không của thiết bị đo, nhiễu đo điện 
áp và nhiễu đo dòng điện qua LiBP. 
- Áp dụng nguyên lý của bộ lọc SPKF để thiết kế thuật toán ước lượng SoC 
cho các mô đun của LiBP khi xét đến trôi điểm không của dòng điện. Việc sử dụng 
02 bộ lọc SPKF để ước lượng SoC cho LiBP, trong đó bộ lọc thứ nhất ước lượng 
SoC trung bình và trôi điểm không của cảm biến đo dòng cho cả LiBP, bộ lọc SPKF 
Thời gian (min) 
D
ò
n
g 
đ
iệ
n
 (
A
) 
Thời gian (min) 
Thời gian (min) 
13 
thứ hai ước lượng độ lệch SoC của các mô đun so với SoC trung bình của cả LiBP 
cho phép giảm được khối lượng và thời gian tính toán. Thuật toán được áp dụng mô 
phỏng với dữ liệu từ thí nghiệm cho bộ pin gồm 7 mô đun nối tiếp, mỗi mô đun gồm 
6 cell nối song song. Qua kết quả mô phỏng trên phần mềm Matlab đã kiểm chứng 
được chất lượng của thuật toán ước lượng SoC cho LiBP đã đề xuất. 
Chương 4. ĐIỀU KHIỂN TỐI ƯU CÂN BẰNG SoC CỦA 
CÁC CELL TRONG LiBP 
4.1 Đặt vấn đề 
Với công nghệ pin Lithium-Ion hiện nay có hai cách để thực hiện cân bằng cell 
là cân bằng chủ động (tích cực) và cân bằng thụ động. Phương pháp cân bằng tích 
cực so với phương pháp cân bằng thụ động có ưu điểm là không gây lãng phí năng 
lượng, tuy nhiên các cấu trúc và giải pháp về điều khiển thường có mức độ phức tạp 
cao hơn, đặc biệt là khi hệ thống pin có nhiều cell mắc nối tiếp, chi phí cũng lớn hơn 
cho việc thiết kế điều khiển, khối lượng tính toán và thời gian cân bằng cũng tăng 
lên. Trong chương bốn, luận án nghiên cứu và áp dụng phương pháp cân bằng SoC 
tích cực dựa trên nguyên lý của mạch chuyển đổi năng lượng hai chiều Cuk với thuật 
toán điều khiển tối ưu SQP để cân bằng SoC cho các cell trong LiBP. 
4.2 Xây dựng mô hình cân bằng SoC của các cell nối nối tiếp. 
4.2.1 Mô hình cân bằng SoC của hai cell nối tiếp. 
4.2.2 Mô hình cân bằng SoC của nhiều cell nối tiếp. 
 Giả thiết một LiBP có n cell mắc nối tiếp, khi đó ta có n-1 bộ cân bằng cell 
CBj, j = 1, 2, , n-1 cho các cell liền kề được thiết kế như Hình 4-3: 
Hình 4-3. Cấu trúc mạch cân bằng cell cho n cell LiB nối tiếp 
Giá trị SoC của cell thứ i (1 ≤ i ≤ n) được cập nhật bằng công thức sau: 
Cell 1 
+ - 
Cell 3 
+ - 
Cell 4 
+ - 
Cell n-1 
+ - 
Cell n 
+ - 
Tải 
Nguồn nạp 
CB1 
CB2 
Cell 2 
+ - 
CB3 
CB4 
CBn-1 
CBn-2 
14 
i i i s
SoC k SoC k SoC k SoC k( 1) ( ) ( ) ( )+ = −∆ −∆ (4.4) 
Đối với n cell công thức cập nhật SoC được xác định tổng quát như sau: 
Cell 1: 
s
D T D T I kT T
SoC k SoC k
Q Q Q
'
11 11 11 12
1 1
( ) ( ) ( )
( 1) ( )
ϕ ϕ
+ = − − − (4.10) 
Cell j: ( j n1< < ) 
i i i i i i i i s
j j
D T D T D T D T I kT T
SoC k SoC k
Q Q Q Q Q
' '
2 1 1 1 2 2 1 2
( ) ( ) ( ) ( ) ( )
( 1) ( )
ϕ ϕ ϕ ϕ
+ = + − + − − (4.11) 
Cell n: 
n n n n s
n n
D T D T I kT T
SoC k SoC k
Q Q Q
'
( 1),1 ( 1),1 ( 1),1 ( 1),2
( ) ( ) ( )
( 1) ( )
ϕ ϕ
− − − −
+ = + − − (4.12) 
Các phương trình (4.10) đến (4.12) là mô hình biểu diễn biến thiên SoC của 
n cell nối tiếp, các SoC của các cell phụ thuộc vào độ rộng xung điều khiển của các 
mạch cân bằng cell (n-1 bộ cân bằng) và dòng tải qua cell. Để biểu diễn mô hình 
quan hệ giữa SoC của các cell và độ rộng xung của các mạch cân bằng cell, ta đặt 
véc tơ biến trạng thái và các véc tơ đầu vào như sau: 
T
n
n
T
n
n
T
n
n
k R SoC k SoC k SoC k
k R D D D
k R D D D
⋯
⋯
⋯
1 2
1
1 11 21 1,1
1
2 12 22 1,2
( ) ( ) ( ) ( )
( )
( )
−
−
−
−
 ∈ =   
 ∈ =   
 ∈ =   
SoC
u
u
 (4.13) 
 Đặt các ma trận hệ thống là: 
n n
n
k
kk R
k
⋯
⋯
⋯
⋯ ⋯ ⋯ ⋱ ⋯
⋯
1
( 1)
21
1
1 0 0 0
( ) 1 0 0
0 ( ) 1 0( )
0 0 0 ( )
β
β
β
× −
−
 − 
 − 
 −∈ =  
 
 
 
 
 
B (4.14) 
n n
k
k
k R k
⋯
⋯
⋯
⋯ ⋯ ⋯ ⋱ ⋯
⋯
'
1
'
2
( 1) '
2 3
( ) 0 0 0
1 ( ) 0 0
( ) 0 1 ( ) 0
0 0 0 1
β
β
β
× −
 
 
 
 
 
∈ =  
 
 
 
 
  
B (4.15) 
Trong đó: 
i i i i
i i i i
i ii i i i
i i i i
f D f D
f D f D
k kf D f D
f D f D
2 1 1 2
'1 1 2 2
1 1 2 2
1 1 2 2
( ) '( )
, ( ) 0 , '( ) 0
( ) , ( ) ,( ) '( )
0, ( ) 0 0, '( ) 0
β β
   ≠ ≠  = = 
  = =   
Đặt các véc tơ: 
15 
( )
( )
T
n
n n
T
n
n n
T
n
s s s s
k R f D T f D T f D T
k R f D T f D T f D T
k R I k T I k T I k T
⋯
⋯
⋯
1
1 1 11 11 21 21 1,1 1,1
1 ' ' '
2 2 12 12 22 22 1,2 1,2
( ) ( ) ( ) ( )
( ) ( ) (( ) (( )
( ) ( ) ( ) ( )
−
− −
−
− −
 ∈ =   
 ∈ =   
 ∈ =   
f u
f u
I
 (4.16) 
Mô hình SoC các cell trong hệ thống cân bằng cell được viết tổng quát như sau: 
( ) ( ) sk k Q kT k Q kT k Q k
1 1 1
1 1 1 2 2 2
( 1) ( ) ( ) ( ) ( ) ( ) ( )− − −+ = + + +SoC SoC B f u B f u I (4.17) 
4.3 Điều khiển tối ưu cân bằng cell cho LiBP 
4.3.1 Thiết lập bài toán điều khiển cân bằng SoC tối ưu 
 Mục tiêu của bài toán điều khiển tối ưu là điều khiển cân bằng SoC của các 
cell sao cho tổn thất năng lượng là nhỏ nhất, có nghĩa là phải điều khiển cân bằng 
SoC của các cell sao cho cực tiểu hóa bình phương sai lệch SoC của các cell so với 
giá trị SoC trung bình của các cell được biểu diễn bằng công thức: 
( )
n
i SoC
i
SoC M
2
1
min
=
−∑ (4.18) 
 Để đảm bảo điều kiện làm việc bình thường, mục tiêu sau liên quan đến n - 1 
bộ cân bằng cell cần được thực hiện: 
i i
n n
L L i i i i
i i
I I D D
1 2
1 12 2
'
1 1 2 1
1 1
min =min ( ) ( )ϕ ϕ
− −
= =
   − −     ∑ ∑ (4.20) 
thỏa mãn các ràng buộc thiết lập về mặt giới hạn trong bài toán điều khiển tối ưu. 
Để thực hiện bài toán điều khiển tối ưu này, ta sử dụng hàm mục tiêu được 
thiết lập từ hai điều kiện cực tiểu hóa (4.18) và (4.20) như sau: 
( )
n n
i i j i i
i j
J k k k p SoC k SoC k q k k
12 2
'
1 2 1 1 2 2
1 1
( ), ( ), ( ) ( 1) ( 1) ( ( )) ( ( ))ϕ ϕ
−
= =
   = + − + + −     ∑ ∑SoC u u u u (4.24) 
Hàm mục tiêu (4.24) có thể được viết dưới dạng toàn phương như sau: 
( ) ( ) ( )
( ) ( )
T
n n
T
J k k k k SoC k k SoC k
k k k k
1 2 1 1
1 1 2 2 1 1 2 2
( ), ( ), ( ) ( 1) ( 1) ( 1) ( 1)
 ( ( )) ( ( )) ( ( )) ( ( )) 
× ×
= + − + + − +
+ − −
SoC u u SoC I P SoC I
f u f u Q f u f u
 (4.25) 
 Tín hiệu điều khiển tối ưu cân bằng cell u1(k) và u2(k) đưa đến n-1 mạch điều 
khiển cân bằng cell bằng cách giải bài toán tối ưu sau: 
( )J k k k1 2( ), ( ), ( ) min→SoC u u (4.27) 
với động học của SoC của các cell tại các thời điểm tiếp theo được xác định: 
( ) ( ) sk k Q kT k Q kT k Q k
1 1 1
1 1 1 2 2 2
( 1) ( ) ( ) ( ) ( ) ( ) ( )− − −+ = + + +SoC SoC B f u B f u I (4.28) 
thỏa mãn các điều kiện ràng buộc: 
( ) ( ) skT k kT k kmin 1 1 1 2 2 2 max( ) ( ) ( ) ( ) ( )≤− − + ≤I B f u B f u I I (4.29) 
n n
SoC k SoC
min 1,1 max 1,1
( 1)
− −
< + <I SoC I (4.30) 
16 
k k
1 2
( ) ( )× =u u 0 (4.31) 
m n
k k D
1 2 ax 1,1
( ), ( )
−
≤ ≤0 u u I (4.32) 
4.3.2 Thuật toán giải bài toán điều khiển tối ưu cân bằng cell 
 Xét trong một chu kỳ điều khiển của bộ điều khiển cân bằng cell, bài toán 
điều khiển tối ưu cân bằng cell được xem như là bài toán điều khiển tối ưu phi tuyến 
tĩnh, vì trong