Tóm tắt Luận án Nghiên cứu sụp đổ lũy tiến của khung bê tông cốt thép toàn khối chịu tác dụng nổ và đề xuất một số giải pháp kháng sập

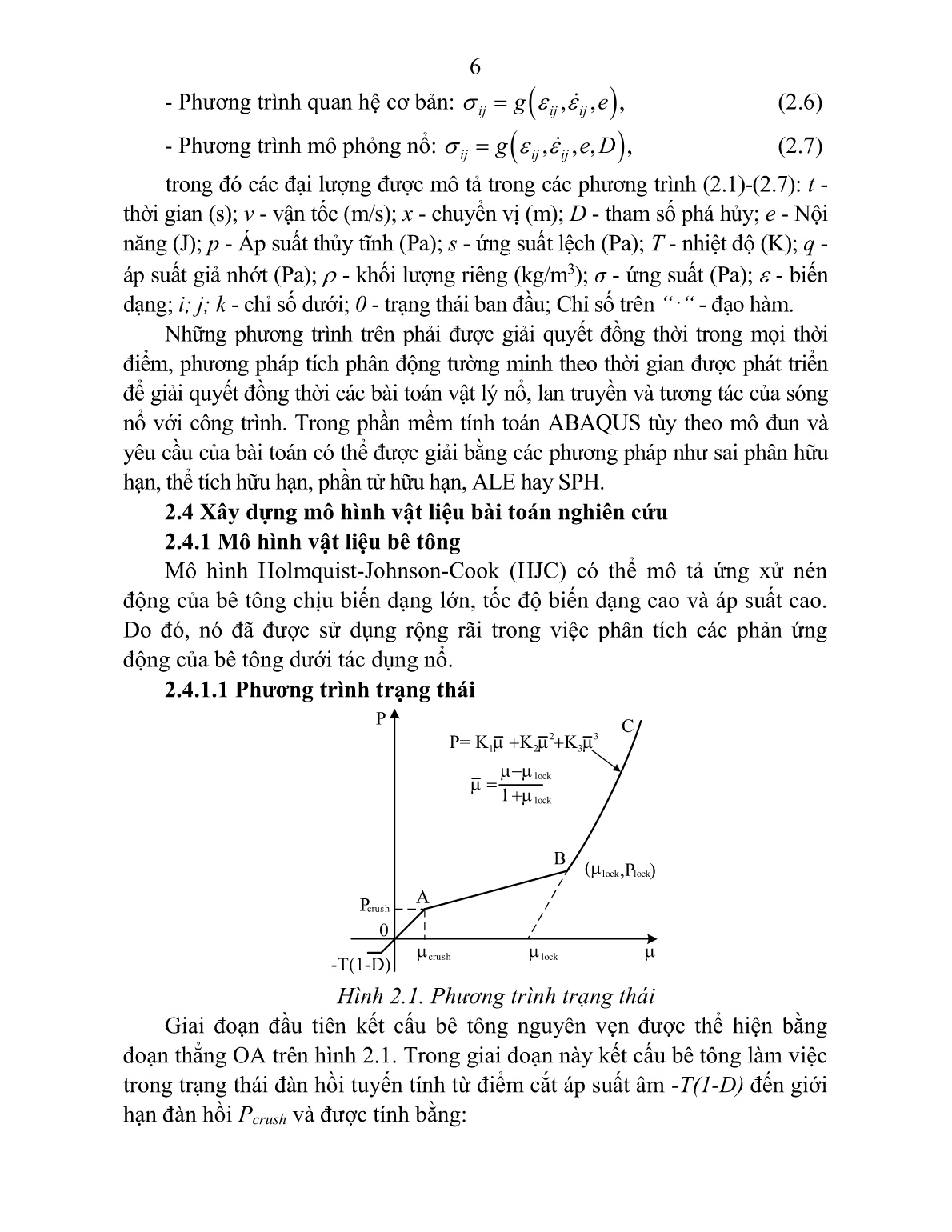
ng như các sở chỉ huy, công trình phòng thủ dân sự,... 
4. Về tải trọng tính toán: Để phục vụ cho giải pháp thiết kế “đường dẫn tải 
thay thế”, khi đặt và giải bài toán, đa số các tác giả chỉ mới quan tâm đến các 
loại tải trọng tĩnh cố định là trọng lượng bản thân của kết cấu và thiết bị, ít quan 
tâm đến chính loại tải trọng gây ra sự phá hoại đột ngột ban đầu của phần tử. 
5. Về mô hình vật liệu và kết cấu: Đối với vật liệu và kết cấu khi nghiên 
cứu các bài toán SĐLT của công trình, chủ yếu quan tâm đến vật liệu đàn 
dẻo: trong đó phần lớn sử dụng mô hình ĐDLT, biến dạng nhỏ, ít sử dụng 
mô hình biến dạng lớn dạng phức tạp hơn và sát thực tế hơn. 
6. Về phương pháp tính toán và phần mềm tính toán: Do lời giải các bài 
toán đặt ra rất phức tạp nên các tác giả chủ yếu trực tiếp sử dụng các phần 
mềm thương mại rất mạnh, được xây dựng trên cơ sở phương pháp PTHH 
như: SAP 2000, ADAPTIC, LS-DYNA, ABAQUS,... 
4 
CHƯƠNG 2. CƠ SỞ LÝ THUYẾT XÂY DỰNG MÔ HÌNH VẬT 
LIỆU, MÔ HÌNH TÍNH TRONG MÔ PHỎNG SỐ PHÂN TÍCH SỤP 
ĐỔ LŨY TIẾN CỦA KẾT CẤU CHỊU TÁC DỤNG NỔ 
2.1 Cơ sở lý thuyết tính toán trong bài toán nghiên cứu 
2.2.1 Vùng thuốc nổ 
Thuốc nổ được sử dụng trong nghiên cứu này là loại thuốc nổ TNT và các 
loại tương đương. Do sự giãn nở rất lớn trong quá trình nổ, nên vùng thuốc nổ 
và các phần tử của sản phẩm thuốc nổ được mô hình hóa và giải theo phương 
pháp lưới Euler hoặc nhờ kỹ thuật hạt không lưới SPH nhằm tránh sự méo mó 
quá lớn của lưới dẫn đến lỗi trong quá trình giải. Do đó thuốc nổ và vùng môi 
trường xung quanh cần phải được thiết lập để mô hình hóa và giải theo cùng 
một phương pháp dạng lưới Euler hoặc kỹ thuật hạt không lưới SPH, trong môi 
trường thiết lập đa vật liệu. 
2.2.2 Vùng gần tâm nổ 
Vùng vật liệu quanh tâm nổ có sự méo mó và biến dạng rất lớn, nếu sử 
dụng phần tử Lagrange thông thường để mô hình hóa, lưới sẽ biến dạng quá 
mức cho phép, phần tử bị lộn ngược lại, thể tích phần tử trở thành âm, dẫn 
đến quá trình tính toán không thể thực hiện được. Hiện nay để giải quyết 
những khó khăn đã nêu, có thể sử dụng phương pháp Lagrangian-Eulerian 
tùy biến ALE (Arbitrary Lagrangian Eulerian) hoặc phương pháp hạt không 
lưới SPH (Smooth Particle Hydrodynamics). Cả hai phương pháp này cho 
phép ta mô phỏng đáp ứng của vùng vật liệu có biến dạng rất lớn. 
2.2.3 Vùng không khí 
Vùng không khí có khả năng bị biến dạng rất lớn nên trong mô phỏng sử 
dụng phương pháp Euler để tính toán. Với phương pháp Euler vật liệu chảy 
qua lưới nên không xảy ra hiện tượng lưới bị méo mó và biến dạng khi vật 
liệu biến dạng lớn. Lời giải bằng cách sử dụng phương pháp Euler thường 
tính toán tốn nhiều bộ nhớ hơn so với sử dụng phương pháp Lagrange. Với 
phương pháp Lagrange trong quá trình tác động các nút của lưới sẽ biến dạng 
theo sự biến dạng của vật liệu còn với phương pháp Euler các nút của lưới 
được cố định trong không gian (chúng không di chuyển), thay vào đó vật liệu 
được theo dõi khi nó di chuyển qua lưới. 
5 
2.2.4 Vùng kết cấu công trình 
Đối với kết cấu công trình chịu tác dụng của tải trọng nổ, sự biến dạng 
của của các phần tử kết cấu, vị trí của mỗi chất điểm trong môi trường kết 
cấu liên tục có thể được mô tả căn cứ theo tọa độ ban đầu sử dụng phương 
pháp Lagrange, vị trí nghiên cứu khi chất điểm trong môi trường kết cấu 
không liên tục thì sử dụng phương pháp Euler, những vị trí chất điểm nằm 
giao thoa hai vùng môi trường kết cấu trên sử dụng kỹ thuật ALE (Arbitrary 
Lagrangian Eulerian) để giải, chuyển vị, vận tốc và gia tốc của các nút cũng 
như ứng suất và biến dạng của các phần tử trong vùng này nhận được nhờ 
giải các phương trình bảo toàn khối lượng, động lượng và năng lượng. Các 
phương trình này cùng với mô hình vật liệu cụ thể và một tập hợp các điều 
kiện ban đầu, điều kiện biên sẽ cho ta lời giải hoàn chỉnh. 
2.3 Phương pháp phân tích động tường minh theo thời gian 
Khi tính toán công trình chịu tác dụng của tải trọng nổ, phương pháp 
phân tích động tường minh theo thời gian sẽ mô tả cơ hệ một cách sát thực 
nhất. Phương pháp này mô phỏng đầy đủ quá trình vật lý nổ, lan truyền 
sóng nổ trong môi trường và tương tác của sóng nổ với kết cấu công trình. 
Hệ công trình và môi trường (không khí, đất) cùng làm việc đồng thời. 
Giải quyết bài toán tương tác này thực chất là giải quyết hệ bài toán vi 
phân đạo hàm riêng cực kỳ phức tạp, trong đó các phương trình phải mô tả 
được các quan hệ vật lý, các định luật bảo toàn, thỏa mãn các điều kiện 
biên và điều kiện ban đầu theo cả trường không gian và thời gian. 
Phương trình của định luật bảo toàn khối lượng: 
( ) 0,i
i
v
t x
  
 
 (2.1) 
Phương trình của định luật bảo toàn động lượng: 
1 ,iji ij i
j j
v vv f
t x x

  
  
 (2.2) 
Phương trình của định luật bảo toàn năng lượng: 
 2
1 ,i i ij ij
i j
E E pv v s
t x t x
 
         
 (2.3) 
Các phương trình bổ trợ cho mô hình hóa: 
- Phương trình ten xơ ứng suất: ( ) ,ij ijp q s (2.4) 
- Phương trình trạng thái: , ,p f e (2.5) 
6 
- Phương trình quan hệ cơ bản: , , ,ij ij ijg e    (2.6) 
- Phương trình mô phỏng nổ: , , , ,ij ij ijg e D    (2.7) 
trong đó các đại lượng được mô tả trong các phương trình (2.1)-(2.7): t - 
thời gian (s); v - vận tốc (m/s); x - chuyển vị (m); D - tham số phá hủy; e - Nội 
năng (J); p - Áp suất thủy tĩnh (Pa); s - ứng suất lệch (Pa); T - nhiệt độ (K); q - 
áp suất giả nhớt (Pa); - khối lượng riêng (kg/m3); σ - ứng suất (Pa);  - biến 
dạng; i; j; k - chỉ số dưới; 0 - trạng thái ban đầu; Chỉ số trên “ .“ - đạo hàm. 
Những phương trình trên phải được giải quyết đồng thời trong mọi thời 
điểm, phương pháp tích phân động tường minh theo thời gian được phát triển 
để giải quyết đồng thời các bài toán vật lý nổ, lan truyền và tương tác của sóng 
nổ với công trình. Trong phần mềm tính toán ABAQUS tùy theo mô đun và 
yêu cầu của bài toán có thể được giải bằng các phương pháp như sai phân hữu 
hạn, thể tích hữu hạn, phần tử hữu hạn, ALE hay SPH. 
2.4 Xây dựng mô hình vật liệu bài toán nghiên cứu 
2.4.1 Mô hình vật liệu bê tông 
Mô hình Holmquist-Johnson-Cook (HJC) có thể mô tả ứng xử nén 
động của bê tông chịu biến dạng lớn, tốc độ biến dạng cao và áp suất cao. 
Do đó, nó đã được sử dụng rộng rãi trong việc phân tích các phản ứng 
động của bê tông dưới tác dụng nổ. 
2.4.1.1 Phương trình trạng thái 
m
P
0
-T(1-D)
A
B
C
m
m 
P= K m K m K m 
mcrush lock
 mlock,P )lock
P crush
m m lock
1 m lock
1 2 3
2 3
Hình 2.1. Phương trình trạng thái 
Giai đoạn đầu tiên kết cấu bê tông nguyên vẹn được thể hiện bằng 
đoạn thẳng OA trên hình 2.1. Trong giai đoạn này kết cấu bê tông làm việc 
trong trạng thái đàn hồi tuyến tính từ điểm cắt áp suất âm -T(1-D) đến giới 
hạn đàn hồi Pcrush và được tính bằng: 
7 
 ; ,crushP K P Pm (2.8) 
trong đó biến dạng thể tích tiêu chuẩn m= / o-1, với và o tương 
ứng khối lượng riêng hiện tại và khối lượng riêng ban đầu. K= Pcrush/ mcrush 
là mô đun đàn hồi với mcrush là biến dạng thể tích ở giới hạn đàn hồi Pcrush. 
Giai đoạn thứ 2 (AB) được gọi là giai đoạn chuyển tiếp, trong giai 
đoạn này các khoảng trống không khí dần dần bị nén ra khỏi bê tông và 
biến dạng thể tích dẻo tạo ra phá hủy khi nén cho đến khi đạt đến điểm 
(mlock, Plock), được thể hiện như sau: 
Quá trình gia tải: P = Pcrush + Klock(m - mcrush), (2.9) 
trong đó Klock = (Plock - Pcrush)/ (mlock - mcrush) là độ dốc của biểu đồ với 
mlock là biến dạng thể tích ở áp lực nén Plock. 
Quá trình dỡ tải: 11 ,o oP P F K FK m m (2.10) 
trong đó F = (mo - mcrush)/ (mlock - mcrush) là hệ số nội suy; Po là áp lực 
khi biến dạng thể tích đạt đến mo trước khi dỡ tải. 
Giai đoạn thứ 3 (BC) là giai đoạn mà tất cả các lỗ rỗng không khí 
được loại bỏ khỏi bê tông, được giả định là hoàn toàn đàn hồi phi tuyến 
tính và mối quan hệ được biểu thị như sau: 
Quá trình gia tải: 2 31 2 3 ,P K K Km m m (2.11) 
trong đó ( ) / (1 )lock lockm m m m là biến dạng thể tích đã sửa đổi, và 
mlock= grain/ o - 1 là biến dạng thể tích khóa với grain là khối lượng riêng của 
bê tông không có lỗ rỗng không khí. K1, K2, K3 là các hằng số của vật liệu. 
Quá trình dỡ tải: 1 .P K m (2.12) 
2.4.1.2 Mô hình bền 
0*T (1-D)
 1.0*
 >1.0*
D=1(đứt gãy)
D=0(không phá hủy)
 
/
f c
*
P = P/f* c
N
Smax
Hình 2.2. Phương trình mặt dẻo 
Ảnh hưởng của tải trọng đến tốc độ biến dạng và phá hủy được thể hiện: 
8 
 * * *(1 ) 1 ln ,NA D BP C   (2.13) 
trong đó *=/fc và P*=P/fc tương ứng là ứng suất và áp lực tương đương 
đã chuẩn hóa; fc là cường độ nén đơn trục;  và P là ứng suất và áp lực tương 
ứng thực tế; * * */ o    là tỷ lệ biến dạng (trong đó * và *o =1.0s-1 tương ứng 
là tốc độ biến dạng thực tế và tham chiếu). T*=T/fc là độ bền kéo chuẩn hóa, 
trong đó T là độ bền kéo đơn trục. Smax là cường độ lớn nhất chuẩn hóa mà vật 
liệu bê tông có thể chịu được. A, B, N tương ứng là các hằng số vật liệu đại diện 
cho cường độ kết dính chuẩn hóa, hệ số làm cứng áp lực chuẩn hóa và số mũ 
tăng cứng áp lực. C là hệ số tốc độ biến dạng và D (0≤D≤1) phá hủy tích lũy. 
2.4.1.3 Mô hình phá hủy 
0 P*
T*  mpfpf = D (P + T )1 * * D2
 
m pf
pf
D=S  mpfpf
efmin
Hình 2.3. Trạng thái phá huỷ của mô hình HJC 
Phá hủy của mô hình HJC được thể hiện ở hình 2.3, được tích lũy từ cả 
biến dạng dẻo tương đương và biến dạng dẻo thể tích, được tính bằng công 
thức: 
 ,p pf f
p p
D
 m
 m
  (2.14) 
trong đó, p và mp tương ứng là số gia biến dạng dẻo tương đương 
và biến dạng dẻo thể tích. f fp p m là tổng hợp biến dạng dẻo dưới áp lực 
không đổi, được xác định bằng: 
 2* *1 min( ) ,
Df f
p p fD P T e m (2.15) 
trong đó efmin là hằng số hư hỏng của bê tông, là điểm tới hạn của trạng 
thái biến dạng dẻo do thí nghiệm lặp. D1 và D2 là các hằng số phá hủy. 
2.4.1.4 Tham số mô hình vật liệu bê tông 
Các thông số của phương trình trạng thái, mô hình bền và mô hình phá 
hủy của bê tông được xác định bằng thí nghiệm được trình bày ở chương 3. 
9 
2.4.2 Mô hình vật liệu thép 
2.4.2.1 Phương trình trạng thái 
 Phương trình trạng thái dạng tuyến tính của cốt thép được mô tả bằng 
định luật Hooke theo phương trình: ,p Em (2.16) 
trong đó: 
0
1 m
 ; E là mô đun đàn hồi của cốt thép. 
2.4.2.2 Mô hình bền 
 Cốt thép sử dụng trong kết cấu được mô tả bởi mô hình bền Johnson-
Cook. Với mô hình này, ứng suất chảy của vật liệu thay đổi phụ thuộc vào 
biến dạng, tốc độ biến dạng và nhiệt độ có dạng sau: 
 *1 ln 1 ,t tn mt t p t p HY A B C T  (2.17) 
trong đó: p là biến dạng dẻo; *p là tốc độ biến dạng dẻo; HT là nhiệt 
độ tương đương, /H room melt roomT T T T T ; roomT là nhiệt độ phòng; 
meltT là nhiệt độ nóng chảy; At, Bt, Ct, nt và mt là các hằng số vật liệu. 
2.4.2.3 Mô hình phá hủy 
Cốt thép là vật liệu đàn dẻo sử dụng mô hình phá hủy do Johnson-
Cook đề xướng, sự phá hủy biến dạng động học của vật liệu là hàm của áp 
lực, tốc độ biến dạng và nhiệt độ như sau: 
f
D 

  với *3 *1 2 4 5
0
1 ln 1 ,Df D D e D D T
 



 (2.18) 
trong đó:  là lượng gia tăng biến dạng dẻo tương ứng với lượng gia 
tăng tải trọng; f là biến dạng tương đương tại thời điểm bị phá hủy; * là 
giá trị trung bình ứng suất; 0,   là tốc độ biến dạng và tốc độ biến dạng 
tham chiếu; T* là tỉ số nhiệt độ; D1, D2, D3, D4, D5 là các hằng số vật liệu. 
Theo mô hình phá hủy này vật liệu được giả định là nguyên vẹn cho 
đến khi tổng biến dạng đạt đến giá trị phá hủy f (D=1.0). 
2.4.2.4 Tham số mô hình vật liệu thép 
Các tham số của phương trình trạng thái, mô hình bền, mô hình phá 
hủy và tham số mô hình vật liệu của thép được lấy theo. 
2.4.3 Mô hình vật liệu nổ TNT 
Để mô hình hóa hiện tượng nổ và quá trình lan truyền áp lực sóng nổ, 
sử dụng phương trình trạng thái do Lee – Tarver và Jones - Wilkins - Lee 
đề xuất. Theo đó phương trình trạng thái của thuốc nổ TNT và chất nổ 
tương đương có dạng như sau: 
10 
 1 2
1 2
(1 ) (1 ) ,tn tnr v r v tntn tn tn tn
tn tn tn
Ep A E B E
r v r v v
  (2.19) 
trong đó: p là áp suất thủy tĩnh; tn = 1/ là thể tích riêng; ρ là khối 
lượng riêng thuốc nổ TNT; Atn, Btn, r1, r2,  là các hằng số đoạn nhiệt được 
xác định từ thí nghiệm; Etn - năng lượng trên đơn vị thể tích. 
2.4.4 Mô hình không khí 
Để mô hình hóa không khí dùng phương trình trạng thái không khí thể 
hiện theo công thức: 
2 3 2
0 1 2 3 4 5 6( ) .kkp C C C C C C C Em m m m (2.20) 
Phương trình trạng thái khí lý tưởng được rút gọn như công thức 
(2.22) với C1 + C2 + C3 + C6 = 0 và C0 = C1 = γ-1: 
 0( 1) / ,kkp E (2.21) 
trong đó: Ekk là nội năng của đơn vị thể tích; μ là hệ số nhớt động; C0, C1 
, C2 , C3 , C4 , C5 , C6 là các hằng số; γ là hệ số nhiệt dung riêng không khí; ρ0 
là khối lượng riêng ban đầu không khí; ρ là khối lượng riêng của không khí. 
2.5 Kết luận của chương 2 
Trong chương 2, tác giả đã trình bày cơ sở lý thuyết để mô phỏng tính 
toán SĐLT cho công trình chịu tác dụng của tải trọng nổ, xây dựng mô hình 
vật liệu, mô hình tính trong mô phỏng số bằng phần mềm ABAQUS. Cụ thể 
tác giả đã trình bày phương pháp phân tích động tường minh theo thời gian, 
lựa chọn mô hình cho các vật liệu (mô hình HJC cho bê tông, mô hình 
Johnson-Cook cho cốt thép, mô hình hóa hiện tượng nổ sử dụng phương 
pháp SPH với phương trình trạng thái do Lee - Tarver và Jones - Wilkins - 
Lee đề xuất, phương trình trạng thái khí lý tưởng cho không khí), giải pháp 
tương tác giữa các vùng và điều kiện biên của bài toán nghiên cứu. 
CHƯƠNG 3. NGHIÊN CỨU THỰC NGHIỆM XÁC ĐỊNH CÁC 
THAM SỐ MÔ HÌNH VẬT LIỆU VÀ HIỆU CHỈNH MÔ HÌNH 
TÍNH TRONG PHÂN TÍCH SỰ SỤP ĐỔ LŨY TIẾN CỦA CÔNG 
TRÌNH CHỊU TẢI TRỌNG NỔ 
3.1 Xác định tham số mô hình vật liệu trong bài toán nghiên cứu 
3.1.1 Tham số mô hình vật liệu bê tông 
Mô hình vật liệu bê tông được áp dụng là mô hình Holmquist - 
Johnson - Cook. Dựa vào các thí nghiệm, 19 tham số của mô hình HJC 
được xác định bằng phương pháp do Holmquist và cộng sự đề xuất. Các 
thí nghiệm nén đơn trục và thí nghiệm lặp cũng như các thí nghiệm ép chẻ 
11 
và nén ba trục được thực hiện bằng máy nén ba trục tại phòng thí nghiệm 
của Bộ môn Cơ sở Kỹ thuật công trình/ Viện Kỹ thuật công trình đặc biệt/ 
Học viện Kỹ thuật Quân sự. 
Từ các thí nghiệm thực hiện được các tham số của mô hình HJC cho 
bê tông B25 được xác định và liệt kê trong bảng 3.1: 
Bảng 3.1. Các tham số mô hình vật liệu bê tông thí nghiệm 
 (kg/m3) G (Pa) A B C N efmin 
2406 11,292 x109 0,79 1,405 0,007 1,085 0,0016 
T (Pa) fc (Pa) Smax Pcrush (Pa) mcrush Plock (Pa) mlock 
3,24 x106 41,305 x106 7 13,768 x106 0,0007 1 x109 0,08 
D1 D2 K1 (Pa) K2 (Pa) K3 (Pa) 
0,04 1,0 85x109 -171 x109 208 x109 
3.1.2 Tham số mô hình vật liệu thép 
Sử dụng mô hình phá hủy do Johnson-Cook đề xuất, các tham số của 
phương trình trạng thái, mô hình bền, mô hình phá hủy của cốt thép (tương 
đương thép CII) được lấy theo bảng 3.2. 
Bảng 3.2. Các tham số mô hình vật liệu thép 
E (MPa)  At (MPa) Bt (MPa) nt Tmelt (K) TH (K) mt 
200000 0,3 263 130 0,0915 1800 293,2 1 
 o (kg/m3) Ct D D1 D2 D3 D4 D5 
7850 0,017 1 0,05 3,44 2,12 0,002 0,61 
3.1.3 Tham số mô hình vật liệu thuốc nổ TNT 
Để mô hình hóa hiện tượng nổ và quá trình lan truyền áp lực sóng nổ, 
sử dụng phương trình trạng thái do Lee – Tarver và Jones - Wilkins - Lee 
đề xuất với các tham số: tn = 1/ o là thể tích riêng; ρo là khối lượng riêng 
thuốc nổ TNT; Atn, Btn, r1, r2,  là các hằng số đoạn nhiệt được xác định từ 
thí nghiệm, vn - tốc độ nổ; Etn - năng lượng trên đơn vị thể tích; PCJ - áp 
lực nổ. Giá trị cụ thể các tham số được liệt kê trong bảng 3.3. 
Bảng 3.3. Tham số mô hình vật liệu TNT 
ρo (kg/m3) vn (m/s) PCJ (kPa) Atn (kPa) Btn (kPa) 
1650 6930 2,1x107 3,7377x108 3,73471x106 
r1 r2 ω tn Etn (kJ/m3) 
4,15 0,9 0,35 1/1650 6x106 
12 
3.1.4 Tham số mô hình không khí 
Để mô hình hóa không khí dùng phương trình trạng thái khí lý tưởng với 
các tham số như bảng 3.4, trong đó: Ekk là nội năng của đơn vị thể tích; C4, C5 là 
các hằng số; mo là khối lượng tương đối; ρo là khối lượng riêng của không khí. 
Bảng 3.4. Tham số mô hình vật liệu không khí 
ρ (kg/m3) E0 (J/m3) mo (kg/m3) C4 C5 
1,23 2,58x105 1,0 0,4 0,4 
 3.2 Thử nghiệm nổ tại hiện trường và mô phỏng số để xác nhận 
mô hình vật liệu, hiệu chỉnh mô hình tính của bài toán nghiên cứu 
 Tác giả tiến hành thử nghiệm nổ tại hiện trường để phá hoại cấu kiện bê 
tông cốt thép thí nghiệm tiết diện 0,2x0,2m, dài 1,5m được gia cường bằng 4 
thanh thép 14, cốt đai 6a200 với chiều dày bảo vệ 0,01m bằng phương 
pháp nổ tiếp xúc và nổ gần. Qua đó xác định được thực trạng bị phá hoại và 
biến dạng tại các điểm đo của cấu kiện. Sau đó tiến hành mô phỏng số bằng 
phần mềm ABAQUS so sánh kết quả giữa mô phỏng với thử nghiệm. 
Mô hình thử nghiệm chế tạo tại xưởng bê tông đúc sẵn Chèm, kích 
thước và chất lượng đảm bảo đúng theo yêu cầu bài toán, sau đó được vận 
chuyển đến thao trường của Học viện KTQS tại Hòa Lạc. Tại thao trường 
tiến hành làm công tác chuẩn bị như hình 3.1, mô hình thử nghiệm nổ tiếp 
xúc với lượng nổ có khối lượng 200gam thuốc nổ TNT (hình 3.2) và mô 
hình thử nghiệm nổ gần trong không khí với khối lượng 1600gam thuốc nổ 
TNT treo chính giữa cách cấu kiện BTCT 300mm (hình 3.3). 
Hình 3.1. Cấu kiện cột bê tông cốt thép và gối đỡ thí nghiệm 
13 
Hình 3.2. Mô hình thử nghiệm nổ tiếp xúc 
Hình 3.3. Mô hình thử nghiệm nổ gần 
3.3 Mô phỏng số sự phá hủy cấu kiện bê tông cốt thép chịu tác 
dụng nổ tiếp xúc và nổ gần 
Tác giả tiến hành thực hiện mô phỏng số bằng phần mềm ABAQUS. Bê 
tông được mô tả như phần tử khối trong khi phần tử thanh áp dụng cho thanh 
thép. Lưới bê tông được chia mịn với kích thước 5mm. Lưới thép chịu lực và 
thép đai cũng được chia mịn với kích thước 5mm. Trong bài toán nổ tiếp xúc, 
thuốc nổ được mô phỏng bằng phương pháp SPH; Trong bài toán nổ gần, thuốc 
nổ được tính theo mô hình CONWEP (UFC 3-340-2). Điều kiện biên: Cấu kiện 
BTCT được liên kết trên 2 gối ( 1 2 3ur ur 0u ) (hình 3.4). 
 (a) Mô hình nổ tiếp xúc 
(b) Mô hình nổ gần 
Hình 3.4. Mô hình hình học mô phỏng số tiếp xúc và nổ gần 
14 
3.4 Phân tích và so sánh kết quả trong trường hợp nổ tiếp xúc 
Kết quả thí nghiệm thực và mô phỏng số như trong hình 3.5, 3.6, 3.7 và bảng 3.5. 
Hình 3.5. Kích thước vùng phá hủy trên mô hình thử nghiệm và mô phỏng số 
Hình 3.6. Biến dạng tại điểm 1 trên mô hình thử nghiệm và mô phỏng số 
Hình 3.7. Biến dạng tại điểm 2 trên mô hình thử nghiệm và mô phỏng số 
Bảng 3.5. So sánh kết quả trên mô hình thử nghiệm và mô phỏng số 
 Mô phỏng số Thử nghiệm Sai khác 
Vùng phá hủy giữa cấu kiện (mm) 264 285 7,4% 
Vùng phá hủy mặt trên cấu kiện (mm) 612 650 5,8% 
Vùng phá hủy mặt dưới cấu kiện (mm) 684 710 3,7% 
Biến dạng dọc trục điểm 1 0,115 0,109 5,5% 
Biến dạng dọc trục điểm 2 0,211 0,236 10,6% 
15 
 3.5 Phân tích và so sánh kết quả trong trường hợp nổ gần 
Kết quả thí nghiệm thực và mô phỏng số như trong hình 3.8, 3.9 và bảng 3.6. 
Hình 3.8. Kích thước vùng phá hủy trên mô hình thử nghiệm và mô phỏng số 
Hình 3.9. Biến dạng tại điểm 1, 2 trên mô hình thử nghiệm và mô phỏng số 
Bảng 3.6. So sánh kết quả trên mô hình thử nghiệm và mô phỏng số 
 Mô phỏng số Thử nghiệm Sai khác 
Chiều sâu phễu chấn sụp (mm) 125 130 3,85% 
Chiều dài phễu chấn sụp (mm) 780 750 4,0% 
Vùng phá hủy mặt bên (mm) 320 400 20,0% 
Biến dạng dọc trục điểm 1 0,2705 0,2376 19,0% 
Biến dạng dọc trục điểm 2 0,2849 0,2394 13,8% 
3.6 Kết luận của chương 3 
Trong chương 3, tác giả đã trình bày nghiên cứu thí nghiệm trong 
phòng thí nghiệm xác định các tham số mô hình vật liệu và nổ thử nghiệm 
ngoài hiện trường kết hợp với mô phỏng số bằng phần mềm ABAQUS để 
hiệu chỉnh các tham số mô hình vật liệu, mô hình tính. 
Các kết quả thu được khẳng định tính hợp lý khi sử dụng mô hình vật 
liệu Holmquist-Johnson-Cook cho bê tông, mô hình vật liệu Johnson-Cook 
cho cốt thép, mô hình vật liệu nổ TNT, mô hình không khí trong phân tích 
kết cấu bê